În geometrie hipercub- aceasta n-analogia dimensională a pătratului ( n= 2) și cubul ( n= 3). Este o formă închisă, convexă, formată din grupuri de linii paralele situate la marginile opuse ale formei și conectate între ele în unghi drept.

Această cifră este cunoscută și ca tesseract(teseract). Tesseract se referă la un cub, așa cum un cub se referă la un pătrat. Mai formal, un tesseract poate fi descris ca un politop cu patru dimensiuni convex obișnuit (politop) a cărui limită constă din opt celule cubice.

Conform Oxford English Dictionary, tesseract a fost inventat în 1888 de Charles Howard Hinton și folosit în cartea sa A New Era of Thought. Cuvântul a fost format din grecescul „τεσσερες ακτινες” („patru raze”), există patru axe de coordonate. În plus, în unele surse, a fost numită aceeași cifră tetracub(tetracub).

n-hipercubul dimensional mai este numit n-cub.

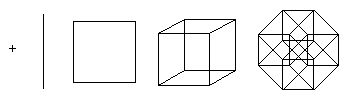
Un punct este un hipercub de dimensiunea 0. Dacă mutați un punct cu o unitate de lungime, obțineți un segment de unitate de lungime - un hipercub de dimensiunea 1. În plus, dacă mutați un segment cu o unitate de lungime în direcția perpendiculară pe direcția segmentului se obține un cub - un hipercub de dimensiunea 2. Deplasând un pătrat cu o unitate de lungime în direcția perpendiculară pe planul pătratului, se obține un cub - un hipercub de dimensiunea 3. Acest proces poate fi generalizat la orice număr de dimensiuni. De exemplu, dacă mutați un cub cu o unitate de lungime în a patra dimensiune, obțineți un tesseract.

Familia hipercuburilor este una dintre puținele poliedre regulate care pot fi reprezentate în orice dimensiune.

Elemente de hipercub

Hipercubul de dimensiune n are 2 n„laturi” (linia unidimensională are 2 puncte; pătrat bidimensional - 4 laturi; cub tridimensional - 6 fețe; tesseract cu patru dimensiuni - 8 celule). Numărul de vârfuri (puncte) ale hipercubului este 2 n(de exemplu, pentru un cub - 2 3 vârfuri).

Cantitate m-hipercuburi dimensionale pe margine n-cubul este egal

De exemplu, marginea unui hipercub conține 8 cuburi, 24 de pătrate, 32 de margini și 16 vârfuri.

Elemente de hipercuburi

n-cub	Nume	Vertex (marginea 0)	Margine (1 parte)	Margine (2 laturi)	Celulă (3 laturi)	(4 laturi)	(5 laturi)	(6 laturi)	(7 laturi)	(8 laturi)
0-cub	Punct	1
1-cub	Secțiune	2	1
2-cub	Pătrat	4	4	1
3-cub	cub	8	12	6	1
4-cub	Teseract	16	32	24	8	1
5-cub	Penterakt	32	80	80	40	10	1
6-cub	Hexeract	64	192	240	160	60	12	1
7-cub	Hepteract	128	448	672	560	280	84	14	1
8-cub	Octect	256	1024	1792	1792	1120	448	112	16	1
9-cub	Generact	512	2304	4608	5376	4032	2016	672	144	18

Proiecția avionului

Formarea unui hipercub poate fi reprezentată în felul următor:

• Două puncte A și B pot fi conectate pentru a forma un segment de dreaptă AB.
• Două segmente de linie paralelă AB și CD pot fi conectate pentru a forma un pătrat ABCD.
• Două pătrate paralele ABCD și EFGH pot fi conectate pentru a forma un cub ABCDEFGH.
• Două cuburi paralele ABCDEFGH și IJKLMNOP pot fi conectate pentru a forma hipercubul ABCDEFGHIJKLMNOP.

Această ultimă structură nu este ușor de imaginat, dar este posibilă reprezentarea proiecției sale pe un spațiu 2D sau 3D. Mai mult decât atât, proiecțiile pe un plan 2D pot fi mai utile prin posibilitatea de a rearanja pozițiile vârfurilor proiectate. În acest caz, puteți obține imagini care nu mai reflectă relațiile spațiale ale elementelor din tesseract, dar ilustrează structura conexiunilor de vârf, ca în exemplele de mai jos.

Prima ilustrație arată cum, în principiu, un tesseract se formează prin unirea a două cuburi. Această diagramă este similară cu diagrama pentru crearea unui cub de două pătrate. A doua diagramă arată că toate marginile teseractului au aceeași lungime. Această schemă vă obligă și să căutați cuburi conectate între ele. În cea de-a treia diagramă, vârfurile teseractului sunt situate în conformitate cu distanțele de-a lungul marginilor față de punctul de jos. Această schemă este interesantă prin faptul că este folosită ca schemă de bază pentru topologia rețelei de conectare a procesoarelor atunci când se organizează calculul paralel: distanța dintre oricare două noduri nu depășește 4 lungimi de margine și există multe moduri diferite de a echilibra sarcina.

Hipercubul în art

Hipercubul a apărut în literatura științifico-fantastică încă din 1940, când Robert Heinlein, în povestea „Și a construit o casă strâmbă”, a descris o casă construită în formă de teseract. În poveste, acest Mai departe, această casă se prăbușește, transformându-se într-un teseract cu patru dimensiuni. După aceea, hipercubul apare în multe cărți și romane.

Filmul „Cube 2: Hypercube” spune povestea a opt oameni prinși într-o rețea de hipercuburi.

Tabloul lui Salvador Dali „Răstignirea” („Răstignirea (Corpus Hypercubus)”, 1954) îl înfățișează pe Iisus răstignit pe o scanare cu teseract. Acest tablou poate fi văzut la Muzeul Metropolitan de Artă din New York.

Concluzie

Hipercubul este unul dintre cele mai simple obiecte cu patru dimensiuni, prin exemplul căruia se poate observa toată complexitatea și neobișnuirea celei de-a patra dimensiuni. Și ceea ce pare imposibil în trei dimensiuni, eventual în patru, de exemplu, figuri imposibile. Deci, de exemplu, barele unui triunghi imposibil în patru dimensiuni vor fi conectate în unghi drept. Și această figură va arăta așa din toate punctele de vedere și nu va fi distorsionată, spre deosebire de realizările triunghiului imposibil în spațiul tridimensional (vezi.

Dacă ți s-a întâmplat un incident neobișnuit, ai văzut o creatură ciudată sau un fenomen de neînțeles, ai avut un vis neobișnuit, ai văzut un OZN pe cer sau ai devenit victima unei răpiri extraterestre, ne poți trimite povestea ta și va fi publicat pe site-ul nostru ===> .

Doctrina spațiilor multidimensionale a început să apară la mijlocul secolului al XIX-lea. Oamenii de știință au împrumutat ideea spațiului cu patru dimensiuni de la oameni de știință. În lucrările lor, ei au povestit lumii despre minunile uimitoare ale celei de-a patra dimensiuni.

Eroii lucrărilor lor, folosind proprietățile spațiului cu patru dimensiuni, puteau mânca conținutul unui ou fără a deteriora coaja, pot bea o băutură fără a deschide capacul sticlei. Hoții au recuperat comoara din seif prin dimensiunea a patra. Chirurgii au efectuat operații asupra organelor interne fără a tăia țesutul corpului pacientului.

Teseract

În geometrie, un hipercub este o analogie n-dimensională a unui pătrat (n = 2) și a unui cub (n = 3). Analogul cu patru dimensiuni al cubului nostru tridimensional obișnuit este cunoscut sub numele de tesseract. Tesseract se referă la un cub, așa cum un cub se referă la un pătrat. Mai formal, un tesseract poate fi descris ca un poliedru cu patru dimensiuni convex obișnuit a cărui limită constă din opt celule cubice.

Fiecare pereche de fețe 3D neparalele se intersectează pentru a forma fețe 2D (pătrate) și așa mai departe. În cele din urmă, un tesseract are 8 fețe 3D, 24 2D, 32 de muchii și 16 vârfuri.
Apropo, conform Dicționarului Oxford, cuvântul tesseract a fost inventat și folosit în 1888 de Charles Howard Hinton (1853-1907) în cartea sa A New Age of Thought. Mai târziu, unii oameni au numit aceeași figură un tetracubus (greacă tetra - patru) - un cub cu patru dimensiuni.

Construcție și descriere

Să încercăm să ne imaginăm cum va arăta hipercubul fără a părăsi spațiul tridimensional.
În „spațiul” unidimensional - pe o linie - selectați un segment AB de lungime L. Pe un plan bidimensional la o distanță L de AB, trageți un segment DC paralel cu acesta și conectați-le capetele. Rezultatul este un CDBA pătrat. Repetând această operație cu planul, obținem un cub tridimensional CDBAGHFE. Și deplasând cubul în a patra dimensiune (perpendicular pe primele trei) cu o distanță L, obținem hipercubul CDBAGHFEKLJIOPNM.

Într-un mod similar, putem continua raționamentul pentru hipercuburi de un număr mai mare de dimensiuni, dar este mult mai interesant să vedem cum va arăta un hipercub cu patru dimensiuni pentru noi, locuitorii spațiului tridimensional.

Luați un cub de sârmă ABCDHEFG și priviți-l cu un ochi din partea feței. Vom vedea și putem desena două pătrate pe plan (fețele sale apropiate și îndepărtate), conectate prin patru linii - margini laterale. În mod similar, un hipercub cu patru dimensiuni în spațiul tridimensional va arăta ca două „cutii” cubice introduse una în cealaltă și conectate prin opt margini. În acest caz, „cutiile” în sine – fețe tridimensionale – vor fi proiectate pe spațiul „nostru”, iar liniile care le leagă se vor întinde în direcția celei de-a patra axe. De asemenea, puteți încerca să vă imaginați un cub nu în proiecție, ci într-o imagine spațială.

Așa cum un cub tridimensional este format dintr-un pătrat deplasat de lungimea unei fețe, un cub mutat în a patra dimensiune va forma un hipercub. Este limitat de opt cuburi, care în perspectivă vor arăta ca o figură destul de complexă. Același hipercub cu patru dimensiuni poate fi rupt într-un număr infinit de cuburi, la fel cum un cub tridimensional poate fi „tăiat” într-un număr infinit de pătrate plate.

După ce tăiați șase fețe ale unui cub tridimensional, îl puteți extinde într-o formă plată - o măturare. Va avea câte un pătrat pe fiecare parte a feței originale plus încă unul - fața opusă acesteia. Și desfășurarea tridimensională a hipercubului cu patru dimensiuni va consta din cubul original, șase cuburi „crescând” din acesta, plus încă unul - „hiperfața” finală.

Hipercubul în art

Tesseract-ul este o figură atât de interesantă încât a atras în mod repetat atenția scriitorilor și realizatorilor de film.
Robert E. Heinlein a menționat de mai multe ori hipercuburi. În The House That Teale Built (1940), el a descris o casă construită ca o dezvoltare a unui tesseract, iar apoi, din cauza unui cutremur, s-a „format” în a patra dimensiune și a devenit un „adevărat” tesseract. Romanul lui Heinlein Road of Glory descrie o cutie supradimensionată care era mai mare la interior decât la exterior.

Povestea lui Henry Kuttner „Toate tenalele Borogovilor” descrie o jucărie educațională pentru copiii din viitorul îndepărtat, similară ca structură cu un tesseract.

Cubul 2: Hypercube se concentrează pe opt străini prinși într-un hipercub sau o rețea de cuburi interconectate.

Lumea paralelă

Abstracțiile matematice au dat naștere ideii existenței unor lumi paralele. Acestea sunt înțelese ca realități care există simultan cu ale noastre, dar independent de aceasta. O lume paralelă poate fi de diferite dimensiuni, de la o zonă geografică mică până la un întreg univers. Într-o lume paralelă, evenimentele se desfășoară în felul lor, pot diferi de lumea noastră, atât în ​​detalii individuale, cât și în aproape orice. Mai mult, legile fizice ale unei lumi paralele nu sunt neapărat analoge cu legile Universului nostru.

Acest subiect este un teren fertil pentru scriitorii de science fiction.

Tabloul lui Salvador Dali „Răstignirea” înfățișează un teseract. „Răstignirea sau corpul hipercubic” - un tablou al artistului spaniol Salvador Dali, pictat în 1954. Îl înfățișează pe Iisus Hristos răstignit pe o scanare a teseractelor. Pictura este păstrată la Metropolitan Museum of Art din New York

Totul a început în 1895, când Herbert Wells a dezvăluit existența unor lumi paralele pentru fantezie cu povestea sa „A Door in a Wall”. În 1923, Wells a revenit la ideea de lumi paralele și a plasat într-una dintre ele o țară utopică, unde sunt trimise personajele romanului „Oameni ca zei”.

Romanul nu a trecut neobservat. În 1926, povestea lui G. Dent „Împăratul Țării“ dacă „ar fi apărut”. În povestea lui Dent, pentru prima dată, a apărut ideea că ar putea exista țări (lumi) a căror istorie ar putea merge diferit de istoria țărilor reale. în lumea noastră.acestea nu sunt mai puţin reale decât ale noastre.

În 1944, Jorge Luis Borges a publicat povestea Grădina căilor care se bifurcă în cartea sa Povestiri fictive. Aici ideea de ramificare a timpului a fost în cele din urmă exprimată cu cea mai mare claritate.
În ciuda apariției lucrărilor enumerate mai sus, ideea mai multor lumi a început să se dezvolte serios în science-fiction abia la sfârșitul anilor patruzeci ai secolului XX, cam în aceeași perioadă în care a apărut o idee similară în fizică.

Unul dintre pionierii unei noi direcții în science-fiction a fost John Bixby, care a sugerat în povestea sa „One-Way Street” (1954) că între lumi nu te poți deplasa decât într-o singură direcție - după ce ai trecut din lumea ta într-una paralelă, nu te vei întoarce, dar vei trece dintr-o lume în alta. Cu toate acestea, nici o întoarcere la propria lume nu este exclusă - pentru aceasta este necesar ca sistemul de lumi să fie închis.

Romanul lui Clifford Simak „A Ring Around the Sun” (1982) descrie numeroase planete ale Pământului, fiecare existând în propria sa lume, dar pe aceeași orbită, iar aceste lumi și aceste planete diferă între ele doar cu o mică (microsecundă) schimbare in timp... Numeroasele ținuturi vizitate de eroul romanului formează un singur sistem de lumi.

Alfred Bester a exprimat o privire interesantă asupra ramificării lumilor în povestea „The Man Who Killed Mohammed” (1958). „Schimbând trecutul”, a argumentat eroul poveștii, „îl schimbi doar pentru tine”. Cu alte cuvinte, după o schimbare în trecut, apare o ramură a istoriei, în care această schimbare există doar pentru personajul care a făcut schimbarea.

Povestea fraților Strugatsky „Luni începe sâmbătă” (1962) descrie călătoriile personajelor în diferite versiuni ale viitorului descrise de scriitorii de SF - spre deosebire de călătoriile care existau deja în SF către diferite versiuni ale trecutului.

Cu toate acestea, chiar și o simplă enumerare a tuturor lucrărilor în care este atinsă tema lumilor paralele ar dura prea mult. Și, deși scriitorii de science fiction, de regulă, nu fundamentează științific postulatul multidimensionalității, au dreptate cu privire la un lucru - aceasta este o ipoteză care are dreptul de a exista.
A patra dimensiune a teseractului încă ne așteaptă.

Victor Savinov

Dacă ești fan al filmelor Avengers, primul lucru care îți vine în minte când auzi cuvântul „Tesseract” este vasul transparent în formă de cub al Pietrei Infinitului care conține o putere nemărginită.

Pentru fanii Universului Marvel, Tesseract este un cub albastru strălucitor care îi înnebunește pe oameni nu numai de pe Pământ, ci și de pe alte planete. Acesta este motivul pentru care toți Răzbunătorii s-au unit pentru a-i proteja pe pământeni de forțele extrem de distructive ale Teseractului.

Cu toate acestea, trebuie spus următoarele: Tesseract este un concept geometric real, sau mai degrabă, o formă care există în 4D. Acesta nu este doar un cub albastru de la Avengers... este un concept real.

Teseractul este un obiect în 4 dimensiuni. Dar înainte de a-l explica în detaliu, să începem de la început.

Ce este dimensiunea?

Toată lumea a auzit termenii 2D și 3D, reprezentând obiecte bidimensionale sau tridimensionale din spațiu. Dar care sunt acestea?

Măsurarea este pur și simplu direcția în care poți merge. De exemplu, dacă desenați o linie pe o bucată de hârtie, puteți merge fie la stânga/dreapta (axa x), fie în sus/jos (axa y). Astfel, spunem că hârtia este bidimensională, deoarece nu poți merge decât în ​​două direcții.

Există un sentiment de profunzime în 3D.

Acum, în lumea reală, pe lângă cele două direcții menționate mai sus (stânga/dreapta și sus/jos), puteți merge și spre/de la. Prin urmare, se adaugă un sentiment de profunzime în spațiul 3D. Prin urmare, spunem că viața reală este tridimensională.

Un punct poate reprezenta 0 dimensiuni (deoarece nu se mișcă în nicio direcție), o linie reprezintă 1 dimensiune (lungime), un pătrat reprezintă 2 dimensiuni (lungime și lățime), iar un cub reprezintă 3 dimensiuni (lungime, lățime și înălțime). ).

Luați un cub 3D și înlocuiți fiecare față (care este în prezent un pătrat) cu un cub. Așadar! Forma pe care o obțineți este teseract.

Ce este un tesseract?

Mai simplu spus, un tesseract este un cub în spațiu cu 4 dimensiuni. De asemenea, puteți spune că este un analog 4D al unui cub. Este o formă 4D în care fiecare față este un cub.

O proiecție 3D a unui teseract care se rotește de două ori în jurul a două plane ortogonale.
Imagine: Jason Hise

Iată o modalitate simplă de a conceptualiza dimensiunile: un pătrat este bidimensional; prin urmare, fiecare dintre colțurile sale are 2 linii care se extind de la el la un unghi de 90 de grade unul față de celălalt. Cubul este 3D, astfel încât fiecare dintre colțurile sale are 3 linii care coboară din el. La fel, tesseractul este o formă 4D, astfel încât fiecare colț are 4 linii care se extind din el.

De ce este dificil să-ți imaginezi un tesseract?

Din moment ce noi, ca oameni, am evoluat pentru a vizualiza obiectele în trei dimensiuni, orice intră în dimensiuni suplimentare, cum ar fi 4D, 5D, 6D etc., nu are prea mult sens pentru noi, pentru că nu le putem introduce deloc. Creierul nostru nu poate înțelege a 4-a dimensiune în spațiu. Pur și simplu nu ne putem gândi la asta.

Puncte (± 1, ± 1, ± 1, ± 1). Cu alte cuvinte, poate fi reprezentat ca următorul set:

Teseractul este delimitat de opt hiperplane, a căror intersecție cu teseractul însuși își definește fețele tridimensionale (care sunt cuburi obișnuite). Fiecare pereche de fețe 3D neparalele se intersectează pentru a forma fețe 2D (pătrate) și așa mai departe. În cele din urmă, un tesseract are 8 fețe 3D, 24 2D, 32 de muchii și 16 vârfuri.

Descriere populară

Să încercăm să ne imaginăm cum va arăta hipercubul fără a părăsi spațiul tridimensional.

În „spațiul” unidimensional - pe o linie - selectați un segment AB de lungime L. Pe un plan bidimensional la o distanță L de AB, trageți un segment DC paralel cu acesta și conectați-le capetele. Rezultatul este un CDBA pătrat. Repetând această operație cu planul, obținem un cub tridimensional CDBAGHFE. Și deplasând cubul în a patra dimensiune (perpendicular pe primele trei) cu o distanță L, obținem hipercubul CDBAGHFEKLJIOPNM.

Construirea unui tesseract pe un plan

Segmentul unidimensional AB este latura pătratului bidimensional CDBA, pătratul este latura cubului CDBAGHFE, care, la rândul său, va fi latura hipercubului cu patru dimensiuni. Un segment de linie dreaptă are două puncte de limită, un pătrat are patru vârfuri, iar un cub are opt. Astfel, într-un hipercub cu patru dimensiuni, vor exista 16 vârfuri: 8 vârfuri ale cubului original și 8 deplasate în a patra dimensiune. Are 32 de muchii - câte 12 oferă pozițiile inițiale și finale ale cubului original, iar încă 8 muchii vor „desena” cele opt vârfuri ale sale, care s-au mutat în a patra dimensiune. Același raționament se poate face și pentru fețele hipercubului. În spațiul bidimensional, este unul (pătratul însuși), cubul are 6 dintre ele (două fețe din pătratul mutat și alte patru vor descrie laturile sale). Un hipercub cu patru dimensiuni are 24 de fețe pătrate - 12 pătrate ale cubului original în două poziții și 12 pătrate din cele douăsprezece muchii ale sale.

Deoarece laturile unui pătrat sunt 4 segmente unidimensionale, iar laturile (fețele) unui cub sunt 6 pătrate bidimensionale, deci pentru un „cub cu patru dimensiuni” (teseract), laturile sunt 8 cuburi tridimensionale . Spațiile perechilor opuse de cuburi tesseract (adică spațiile tridimensionale cărora le aparțin aceste cuburi) sunt paralele. În figură, acestea sunt cuburi: CDBAGHFE și KLJIOPNM, CDBAKLJI și GHFEOPNM, EFBAMNJI și GHDCOPLK, CKIAGOME și DLJBHPNF.

Într-un mod similar, putem continua raționamentul pentru hipercuburi de un număr mai mare de dimensiuni, dar este mult mai interesant să vedem cum va arăta un hipercub cu patru dimensiuni pentru noi, locuitorii spațiului tridimensional. Să folosim metoda de analogie familiară pentru aceasta.

Luați un cub de sârmă ABCDHEFG și priviți-l cu un ochi din partea feței. Vom vedea și putem desena două pătrate pe plan (fețele sale apropiate și îndepărtate), conectate prin patru linii - margini laterale. În mod similar, un hipercub cu patru dimensiuni în spațiul tridimensional va arăta ca două „cutii” cubice introduse una în cealaltă și conectate prin opt margini. În acest caz, „cutiile” în sine – fețe tridimensionale – vor fi proiectate pe spațiul „nostru”, iar liniile care le leagă se vor întinde în direcția celei de-a patra axe. De asemenea, puteți încerca să vă imaginați un cub nu în proiecție, ci într-o imagine spațială.

Așa cum un cub tridimensional este format dintr-un pătrat deplasat de lungimea unei fețe, un cub mutat în a patra dimensiune va forma un hipercub. Este limitat de opt cuburi, care în perspectivă vor arăta ca o figură destul de complexă. Același hipercub cu patru dimensiuni constă dintr-un număr infinit de cuburi, la fel cum un cub tridimensional poate fi „tăiat” într-un număr infinit de pătrate plate.

După ce tăiați șase fețe ale unui cub tridimensional, îl puteți extinde într-o formă plată - o măturare. Va avea câte un pătrat pe fiecare parte a feței originale plus încă unul - fața opusă acesteia. Și desfășurarea tridimensională a hipercubului cu patru dimensiuni va consta din cubul original, șase cuburi „crescând” din acesta, plus încă unul - „hiperfața” finală.

Proprietățile teseractelor sunt continuarea proprietăților figurilor geometrice de dimensiuni mai mici în spațiul cu patru dimensiuni.

Proiecție

În spațiul bidimensional

Această structură este dificilă pentru imaginație, dar este posibilă proiectarea unui tesseract în spații 2D sau 3D. În plus, proiecția în plan facilitează înțelegerea locației vârfurilor hipercubului. În acest fel, pot fi obținute imagini care nu mai reflectă relații spațiale în cadrul teseractului, dar care ilustrează structura conexiunilor de vârf, ca în următoarele exemple:

A treia imagine prezintă teseractul în vedere izometrică, raportat la punctul de construcție. Această vedere este de interes atunci când se utilizează un tesseract ca bază pentru o rețea topologică pentru a lega mai multe procesoare în calcul paralel.

În spațiul tridimensional

Una dintre proiecțiile teseractului pe spațiul tridimensional este reprezentată de două cuburi tridimensionale imbricate, ale căror vârfuri corespunzătoare sunt conectate prin segmente. Cuburile interioare și exterioare au dimensiuni diferite în spațiul tridimensional, dar în spațiul cu patru dimensiuni sunt cuburi egale. Pentru a înțelege egalitatea tuturor cuburilor teseractului, a fost creat un model de teseract rotativ.

• Cele șase piramide trunchiate de la marginile teseractului sunt imagini de șase cuburi egale. Cu toate acestea, aceste cuburi sunt la un tesseract - ca pătratele (fețele) la un cub. Dar, de fapt, teseractul poate fi împărțit într-un număr infinit de cuburi, ca un cub - într-un număr infinit de pătrate, sau un pătrat - într-un număr infinit de segmente.

O altă proiecție interesantă a teseractului pe spațiul tridimensional este un dodecaedru rombic cu cele patru diagonale desenate, conectând perechi de vârfuri opuse la unghiuri mari romb. În acest caz, 14 din cele 16 vârfuri ale teseractului sunt proiectate în 14 vârfuri ale rombododecaedrului, iar proiecțiile celor 2 rămase coincid în centrul acestuia. Într-o astfel de proiecție pe un spațiu tridimensional, egalitatea și paralelismul tuturor laturilor unidimensionale, bidimensionale și tridimensionale sunt păstrate.

Pereche stereo

O stereopereche a unui tesseract este reprezentată ca două proiecții în spațiul tridimensional. Această imagine tesseract a fost concepută pentru a reprezenta adâncimea ca o a patra dimensiune. O pereche stereo este vizualizată astfel încât fiecare ochi să vadă doar una dintre aceste imagini, apare o imagine stereoscopică care reproduce adâncimea teseractului.

Desfăşurarea teseractului

Suprafața unui teseract poate fi extinsă în opt cuburi (similar cu modul în care suprafața unui cub poate fi extinsă în șase pătrate). Există 261 de teseract diferite care se desfășoară. Desfăşurarea teseractului poate fi calculată prin trasarea colţurilor conectate pe grafic.

Teseract în art

• În New Abbott Plains de Edwine A., hipercubul este povestitorul.
• Într-un episod din Aventurile lui Jimmy Neutron, „băiatul genial” Jimmy inventează un hipercub cu patru dimensiuni identic cu cutia pliabilă din The Road to Glory (1963) de Robert Heinlein.
• Robert E. Heinlein a menționat hipercuburi în cel puțin trei povești științifico-fantastice. În „Casa celor patru dimensiuni” („The House That Teal Built”), el a descris o casă construită ca o dezvoltare a unui tesseract, iar apoi, din cauza unui cutremur, s-a „format” în a patra dimensiune și a devenit un „adevărat”. "teseract.
• Romanul lui Heinlein Road of Glory descrie o cutie supradimensionată care era mai mare la interior decât la exterior.
• Povestea lui Henry Kuttner „Toate tenalele Borogovilor” descrie o jucărie educațională pentru copiii din viitorul îndepărtat, similară ca structură cu un tesseract.
• În romanul lui Alex Garland (), termenul „tesseract” este folosit pentru o desfășurare tridimensională a unui hipercub cu patru dimensiuni, nu hipercubul în sine. Aceasta este o metaforă menită să arate că sistemul de cunoaștere ar trebui să fie mai larg decât cel de cunoaștere.
• Cubul 2: Hypercube se concentrează pe opt străini prinși într-un hipercub sau o rețea de cuburi interconectate.
• Serialul TV Andromeda folosește generatoare de teseract ca dispozitiv de conspirație. Ele sunt concepute în primul rând pentru a manipula spațiul și timpul.
• Tabloul „Răstignirea” (Corpus Hypercubus) de Salvador Dali ().
• Cartea de benzi desenate Nextwave descrie un vehicul care include 5 zone tesseract.
• Pe albumul Voivod Nothingface, una dintre melodii se numește „In my hypercube”.
• În romanul lui Anthony Pierce „Route Cuba”, una dintre lunile care orbitează în jurul Asociației Internaționale de Dezvoltare se numește tesseract, care a fost comprimat în 3 dimensiuni.
• În serialul „Școală” Black Hole „” în al treilea sezon există un serial „Tesseract”. Lucas apasă un buton secret și școala începe să „prindă formă ca un teseract matematic”.
• Termenul „tesseract” și termenul „tesserat”, derivat din acesta, se găsesc în povestea lui Madeleine L'Engle „The Fold of Time”.
• TesseracT este numele unui grup de gentleman britanic.
• În seria de filme Marvel Cinematic Universe, Tesseract este un element cheie al intrigii, un artefact spațial în formă de hipercub.
• În povestea lui Robert Sheckley „Miss Mouse and the Fourth Dimension”, un scriitor ezoteric, o cunoștință a autorului, încearcă să vadă un tesseract, căutând ore întregi la un dispozitiv pe care l-a construit: o minge pe un picior cu tije înfipte în el, pe care sunt plantate cuburi, lipite cu toate simbolurile ezoterice succesive. Povestea menționează opera lui Hinton.
• În filmele Captain America: The Avengers. Teseract-energie a întregului univers

Alte nume

• Hexadekahoron (ing. Hexadecachoron)
• Octohoron (ing. Octachoron)
• Tetracubus
• 4-Cub
• Hypercube (dacă nu este specificat numărul de măsurători)

Note (editare)

Literatură

• Charles H. Hinton. A patra dimensiune, 1904. ISBN 0-405-07953-2
• Martin Gardner, Carnavalul matematic, 1977. ISBN 0-394-72349-X
• Ian Stewart, Concepte de matematică modernă, 1995. ISBN 0-486-28424-7

Legături

In rusa

• Programul Transformator4D. Formarea modelelor de proiecții tridimensionale ale obiectelor cu patru dimensiuni (inclusiv Hypercube).
• Un program care implementează construcția unui tesseract și toate transformările sale afine, cu surse în C++.

În limba engleză

• Mushware Limited - program de inferență Tesseract ( Tesseract Trainer, licență compatibilă cu GPLv2) și first person shooter în spațiu cu patru dimensiuni ( Adanaxis; grafică, mai ales tridimensională; există o versiune sub GPL în arhivele OS).

Poliedre
Corect (solide platonice)
Dodecaedru stelat Icosidodecaedru stelat Icosaedru stelat Poliedru stelat Octaedru stelat
Convex	Corpurile arhimedeene Cuboctaedru Icosidodecaedru Tetraedru trunchiat Octaedru trunchiat Icosaedru trunchiat Icozaedru trunchiat Cub trunchiat Dodecaedru trunchiat Rombocuboctaedru Romboicosododecaedru Rombo-trunchiat Cuboctaedru Rombo-trunchiat Cuboctaedru trunchiat Rombocaedru-truncaedru Cubocaedru truncat Organismele Catalane Rombododecaedru Rombotricontaedru Triakistetraedru Tetrakishexaedru Pentakisdodecaedru Triakisoktaedru Triakisycosaedru Icositeraedru deltoidal Hexcontaedru deltoidal Icostetraedru pentagonal Fără simetrie spațială completă Prismă piramidală Bipiramidă Antiprismă Zonoedru Paralelepiped Romboedru Prismatoid Piramidă trunchiată Pentagondodecaedru paraleloedru
Formule, teoreme, teorie
Alte

Hipercubul și Solidele platonice

Simulați un icosaedru trunchiat („minge de fotbal”) în sistemul „Vector”.
în care fiecare pentagon este delimitat de hexagoane

Icosaedru trunchiat poate fi obținut prin tăierea a 12 vârfuri cu formarea de fețe sub formă de pentagoane regulate. În acest caz, numărul de vârfuri ale noului poliedru crește de 5 ori (12 × 5 = 60), 20 de fețe triunghiulare se transformă în hexagoane regulate (în total fețele devin 20 + 12 = 32), A numărul de muchii crește la 30 + 12 × 5 = 90.

Etape pentru construirea unui icosaedru trunchiat în sistemul „Vector”.

Forme în spațiul 4-dimensional.

--à

--à ?

De exemplu, având în vedere un cub și un hipercub. Există 24 de fețe într-un hipercub. Aceasta înseamnă că un octaedru cu 4 dimensiuni va avea 24 de vârfuri. Deși nu, un hipercub are 8 fețe de cuburi - fiecare are un vârf-centru. Aceasta înseamnă că un octaedru cu 4 dimensiuni va avea 8 vârfuri care sunt mai ușor.

octaedru cu 4 dimensiuni... Este format din opt tetraedre echilaterale și egale,
legate prin patru la fiecare vârf.

Orez. Încercați să simulați
hipersferă-hipersferă în sistemul „Vector”.

Fețe față - spate - bile fără distorsiuni. Încă șase bile - puteți specifica prin elipsoide sau suprafețe pătratice (prin 4 linii de contur ca generatoare) sau prin fețe (mai întâi specificate prin generatoare).

Mai multe trucuri pentru a „construi” o hipersferă
- aceeași „minge de fotbal” în spațiul 4-dimensional

Anexa 2

Pentru politopii convexi, există o proprietate care leagă numărul vârfurilor, muchiilor și fețelor sale, demonstrată în 1752 de Leonard Euler și numită teorema lui Euler.

Înainte de a-l formula, luați în considerare poliedrele pe care le cunoaștem și completați următorul tabel, în care B este numărul de vârfuri, P este muchiile și G este fețele unui politop dat:

Nume poliedru
Piramida triunghiulara
Piramida patruunghiulara
Prisma triunghiulara
Prismă patruunghiulară
n -piramida cărbunelui	n+1	2n	n+1
n -prismă de carbon	2n	3n	n + 2
n -cărbune trunchiat piramidă	2n	3n	n + 2

Acest tabel arată în mod direct că pentru toți politopii selectați este valabilă egalitatea B - P + Γ = 2. Se pare că această egalitate este valabilă nu numai pentru acești politopi, ci și pentru un poliedru convex arbitrar.

teorema lui Euler. Pentru orice politop convex, egalitatea

B - R + G = 2,

unde B este numărul de vârfuri, P este numărul de muchii și G este numărul de fețe ale unui poliedru dat.

Dovada. Pentru a demonstra această egalitate, reprezentăm suprafața unui poliedru dat dintr-un material elastic. Să ștergem (decupăm) una dintre fețele ei și să întindem suprafața rămasă pe un plan. Obținem un poligon (format din muchiile feței îndepărtate a poliedrului), împărțit în poligoane mai mici (formate de celelalte fețe ale poliedrului).

Rețineți că poligoanele pot fi deformate, mărite, reduse sau chiar curbate pe laturile lor, atâta timp cât laturile nu se rupe. Acest lucru nu modifică numărul de vârfuri, muchii și fețe.

Să demonstrăm că pentru împărțirea rezultată a unui poligon în poligoane mai mici, este valabilă următoarea egalitate:

(*) B - R + G "= 1,

unde В este numărul total de vârfuri, Р este numărul total de muchii și Г "este numărul de poligoane incluse în partiție. Este clar că Г" = Г - 1, unde Г este numărul de fețe ale unui poliedru dat.

Să demonstrăm că egalitatea (*) nu se schimbă dacă o diagonală este trasată într-un poligon al partiției date (Fig. 5, a). Într-adevăr, după desenarea unei astfel de diagonale în noua partiție, vor exista B vârfuri, P + 1 muchii, iar numărul de poligoane va crește cu unul. Prin urmare, avem

B - (P + 1) + (G "+1) = B - P + G" .

Folosind această proprietate, desenăm diagonalele care împart poligoanele de intrare în triunghiuri, iar pentru partiția rezultată arătăm că egalitatea (*) este îndeplinită (Fig. 5, b). Pentru a face acest lucru, vom elimina în mod constant marginile exterioare, reducând numărul de triunghiuri. În acest caz, sunt posibile două cazuri:

a) pentru a elimina triunghiul ABC este necesară îndepărtarea a două coaste, în cazul nostru ABși î.Hr;

b) pentru a elimina triunghiulMKNeste necesară îndepărtarea unei margini, în cazul nostruMN.

În ambele cazuri, egalitatea (*) nu se va modifica. De exemplu, în primul caz, după ștergerea triunghiului, graficul va fi format din B - 1 vârfuri, P - 2 muchii și G "- 1 poligon:

(B - 1) - (R + 2) + (G "- 1) = B - R + G".

Luați în considerare cel de-al doilea caz pe cont propriu.

Astfel, eliminarea unui triunghi nu schimbă egalitatea (*). Continuând acest proces de ștergere a triunghiurilor, în final, ajungem la o partiție formată dintr-un triunghi. Pentru o astfel de partiție, B = 3, P = 3, Γ "= 1 și, prin urmare, B - P + Γ" = 1. Prin urmare, egalitatea (*) este valabilă și pentru partiția originală, de unde obținem în final că pentru o partiția dată a egalității poligonului (*) este adevărată. Astfel, pentru politopul convex original, egalitatea B - P + Γ = 2 este adevărată.

Un exemplu de poliedru pentru care relația lui Euler nu este valabilă, prezentat în Figura 6. Acest poliedru are 16 vârfuri, 32 de muchii și 16 fețe. Astfel, pentru acest poliedru, egalitatea B - P + Γ = 0 este valabilă.

Anexa 3.

Film Cube 2: Hypercube "(ing. Cube 2: Hypercube) - un film fantastic, continuarea filmului "Cube".

Opt străini se trezesc în camere în formă de cub. Camerele sunt situate în interiorul unui hipercub cu patru dimensiuni. Camerele se mișcă în mod constant prin „teleportare cuantică”, iar dacă urci în camera următoare, atunci revenirea la cea veche este deja puțin probabilă. Într-un hipercub, lumi paralele se intersectează, timpul curge în unele camere în moduri diferite, iar unele camere sunt capcane ale morții.

Intriga imaginii repetă în mare măsură istoria primei părți, care se reflectă și în imaginile unora dintre personaje. Laureatul Nobel Rosenzweig, care a calculat ora exactă a distrugerii hipercubului, moare în încăperile hipercubului.

Critică

Dacă în prima parte oamenii închiși într-un labirint au încercat să se ajute unii pe alții, în acest film este fiecare bărbat pentru el însuși. Există o mulțime de efecte speciale inutile (sunt capcane) care nu leagă logic această parte a filmului cu cea anterioară. Adică, se dovedește că filmul Cube 2 - acesta este un fel de labirint al viitorului 2020-2030, dar nu 2000. În prima parte, tot felul de capcane pot fi create teoretic de o persoană. În a doua parte, aceste capcane sunt un program de calculator, așa-numitul „Realitate Virtuală”.