En geometría hipercubo- eso norte-analógica dimensional del cuadrado ( norte= 2) y cubo ( norte= 3). Es una forma convexa cerrada formada por grupos de líneas paralelas ubicadas en los bordes opuestos de la forma, y ​​conectadas entre sí en ángulos rectos.

Esta figura también se conoce como tesseract(tesseract). Tesseract se refiere a un cubo como un cubo se refiere a un cuadrado. Más formalmente, un tesseract se puede describir como un politopo (politopo) convexo regular de cuatro dimensiones cuyo límite consta de ocho celdas cúbicas.

Según el Oxford English Dictionary, el tesseract fue acuñado en 1888 por Charles Howard Hinton y utilizado en su libro A New Era of Thought. La palabra se formó a partir del griego "τεσσερες ακτινες" ("cuatro rayos"), hay cuatro ejes de coordenadas. Además, en algunas fuentes, la misma figura se denominó tetracubo(tetracubo).

norte-El hipercubo dimensional también se llama n-cubo.

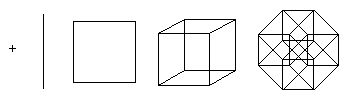
Un punto es un hipercubo de dimensión 0. Si mueves un punto en una unidad de longitud, obtienes un segmento de unidad de longitud, un hipercubo de dimensión 1. Además, si mueves un segmento en una unidad de longitud en la dirección perpendicular a la dirección del segmento, se obtiene un cubo - un hipercubo de dimensión 2. Desplazando un cuadrado en una unidad de longitud en la dirección perpendicular al plano del cuadrado, se obtiene un cubo - un hipercubo de dimensión 3. Este proceso se puede generalizar a cualquier número de dimensiones. Por ejemplo, si mueves un cubo una unidad de longitud en la cuarta dimensión, obtienes un tesseract.

La familia de los hipercubos es uno de los pocos poliedros regulares que se pueden representar en cualquier dimensión.

Elementos de hipercubo

Hipercubo de dimensión norte tiene 2 norte"lados" (la línea unidimensional tiene 2 puntos; cuadrado bidimensional - 4 lados; cubo tridimensional - 6 caras; tesseract de cuatro dimensiones - 8 celdas). El número de vértices (puntos) del hipercubo es 2 norte(por ejemplo, para un cubo - 2 3 vértices).

Cantidad metro-hipercubos dimensionales en la frontera norte-cubo es igual a

Por ejemplo, el borde de un hipercubo contiene 8 cubos, 24 cuadrados, 32 bordes y 16 vértices.

Elementos de hipercubos

n-cubo	Nombre	Vértice (Borde 0)	Borde (1 cara)	Borde (2 caras)	Celda (3 lados)	(4 lados)	(5 lados)	(6 lados)	(7 lados)	(8 lados)
0-cubo	Punto	1
1 cubo	Sección	2	1
2 cubos	Cuadrado	4	4	1
3 cubos	Cubo	8	12	6	1
4 cubos	Tesseract	16	32	24	8	1
5 cubos	Penterakt	32	80	80	40	10	1
6 cubos	Hexeracto	64	192	240	160	60	12	1
7 cubos	Hepterata	128	448	672	560	280	84	14	1
8 cubos	Octract	256	1024	1792	1792	1120	448	112	16	1
9 cubos	Generact	512	2304	4608	5376	4032	2016	672	144	18

Proyección de plano

La formación de un hipercubo se puede representar de la siguiente manera:

• Se pueden conectar dos puntos A y B para formar un segmento de línea AB.
• Se pueden conectar dos segmentos de línea paralelos AB y CD para formar un cuadrado ABCD.
• Se pueden conectar dos cuadrados paralelos ABCD y EFGH para formar un cubo ABCDEFGH.
• Se pueden conectar dos cubos paralelos ABCDEFGH e IJKLMNOP para formar el hipercubo ABCDEFGHIJKLMNOP.

Esta última estructura no es fácil de imaginar, pero es posible representar su proyección en un espacio 2D o 3D. Además, las proyecciones en un plano 2D pueden ser más útiles al poder reorganizar las posiciones de los vértices proyectados. En este caso, puede obtener imágenes que ya no reflejan las relaciones espaciales de los elementos dentro del tesseract, sino que ilustran la estructura de las conexiones de vértices, como en los ejemplos siguientes.

La primera ilustración muestra cómo, en principio, un tesseract se forma uniendo dos cubos. Este diagrama es similar al diagrama para crear un cubo de dos cuadrados. El segundo diagrama muestra que todos los bordes del tesseract tienen la misma longitud. Este esquema también te obliga a buscar cubos conectados entre sí. En el tercer diagrama, los vértices del tesseract se ubican de acuerdo con las distancias a lo largo de los bordes con respecto al punto inferior. Este esquema es interesante porque se utiliza como esquema básico para la topología de red de los procesadores de conexión cuando se organiza la computación en paralelo: la distancia entre dos nodos cualesquiera no excede las 4 longitudes de borde y hay muchas formas diferentes de equilibrar la carga.

Hipercubo en el arte

El hipercubo ha aparecido en la literatura de ciencia ficción desde 1940, cuando Robert Heinlein, en el cuento "Y construyó una casa torcida", describió una casa construida en forma de teseracto. En la historia, este Más allá, esta casa se derrumba, convirtiéndose en un teseracto de cuatro dimensiones. Después de eso, el hipercubo aparece en muchos libros y novelas.

La película "Cube 2: Hypercube" cuenta la historia de ocho personas atrapadas en una red de hipercubos.

La pintura de Salvador Dalí "La crucifixión" ("Crucifixión (Corpus Hypercubus)", 1954) representa a Jesús crucificado en un teseracto. Esta pintura se puede ver en el Museo Metropolitano de Arte de Nueva York.

Conclusión

El hipercubo es uno de los objetos de cuatro dimensiones más simples, en cuyo ejemplo se puede ver toda la complejidad e inusual de la cuarta dimensión. Y lo que parece imposible en tres dimensiones, posiblemente en cuatro, por ejemplo, figuras imposibles. Entonces, por ejemplo, las barras de un triángulo imposible en cuatro dimensiones estarán conectadas en ángulos rectos. Y esta figura se verá así desde todos los puntos de vista, y no se distorsionará, a diferencia de las realizaciones del triángulo imposible en el espacio tridimensional (ver.

Si te sucedió un incidente inusual, viste una criatura extraña o un fenómeno incomprensible, tuviste un sueño inusual, viste un OVNI en el cielo o te volviste víctima de una abducción extraterrestre, puedes enviarnos tu historia y será publicado en nuestro sitio web ===> .

La doctrina de los espacios multidimensionales comenzó a aparecer a mediados del siglo XIX. Los científicos tomaron prestada la idea del espacio de cuatro dimensiones de los científicos. En sus obras, le contaron al mundo sobre las asombrosas maravillas de la cuarta dimensión.

Los héroes de sus obras, utilizando las propiedades del espacio de cuatro dimensiones, podían comer el contenido de un huevo sin dañar la cáscara, beber una bebida sin abrir la tapa de la botella. Los ladrones recuperaron el tesoro de la caja fuerte a través de la cuarta dimensión. Los cirujanos realizaron operaciones en los órganos internos sin cortar el tejido corporal del paciente.

Tesseract

En geometría, un hipercubo es una analogía n-dimensional de un cuadrado (n = 2) y un cubo (n = 3). El análogo de cuatro dimensiones de nuestro cubo tridimensional habitual se conoce como tesseract. Tesseract se refiere a un cubo como un cubo se refiere a un cuadrado. Más formalmente, un tesseract se puede describir como un poliedro convexo regular de cuatro dimensiones cuyo límite consta de ocho celdas cúbicas.

Cada par de caras 3D no paralelas se cruzan para formar caras 2D (cuadrados), y así sucesivamente. Finalmente, un tesseract tiene 8 caras 3D, 24 2D, 32 aristas y 16 vértices.
Por cierto, según el Diccionario Oxford, el tesseract fue acuñado y utilizado en 1888 por Charles Howard Hinton (1853-1907) en su libro A New Age of Thought. Más tarde, algunas personas llamaron a la misma figura un tetracubus (griego tetra - cuatro), un cubo de cuatro dimensiones.

Construcción y descripción

Intentemos imaginar cómo se verá el hipercubo sin dejar un espacio tridimensional.
En un "espacio" unidimensional - en una línea - seleccione un segmento AB de longitud L. En un plano bidimensional a una distancia L de AB, dibuje un segmento DC paralelo a él y conecte sus extremos. El resultado es un CDBA cuadrado. Repitiendo esta operación con el plano, obtenemos un cubo tridimensional CDBAGHFE. Y desplazando el cubo en la cuarta dimensión (perpendicular a las tres primeras) en una distancia L, obtenemos el hipercubo CDBAGHFEKLJIOPNM.

De manera similar, podemos continuar el razonamiento para hipercubos de un mayor número de dimensiones, pero es mucho más interesante ver cómo se verá un hipercubo de cuatro dimensiones para nosotros, habitantes del espacio tridimensional.

Tome un cubo de alambre ABCDHEFG y mírelo con un ojo desde el costado de la cara. Veremos y podemos dibujar dos cuadrados en el plano (sus caras cercanas y lejanas), conectadas por cuatro líneas: bordes laterales. De manera similar, un hipercubo de cuatro dimensiones en un espacio tridimensional se verá como dos "cajas" cúbicas insertadas entre sí y conectadas por ocho bordes. En este caso, las "cajas" en sí mismas, caras tridimensionales, se proyectarán en "nuestro" espacio, y las líneas que las conectan se estirarán en la dirección del cuarto eje. También puede intentar imaginar un cubo no en proyección, sino en una imagen espacial.

Así como un cubo tridimensional está formado por un cuadrado desplazado por la longitud de una cara, un cubo desplazado a la cuarta dimensión formará un hipercubo. Está limitado por ocho cubos, que en perspectiva parecerán una figura bastante compleja. El mismo hipercubo de cuatro dimensiones se puede dividir en un número infinito de cubos, al igual que un cubo de tres dimensiones se puede "cortar" en un número infinito de cuadrados planos.

Después de cortar seis caras de un cubo tridimensional, puede expandirlo a una forma plana: un barrido. Tendrá un cuadrado a cada lado de la cara original más uno más, la cara opuesta. Y el despliegue tridimensional del hipercubo de cuatro dimensiones consistirá en el cubo original, seis cubos "creciendo" de él, más uno más: la "hipercara" final.

Hipercubo en el arte

El Tesseract es una figura tan interesante que ha atraído repetidamente la atención de escritores y cineastas.
Robert E. Heinlein mencionó los hipercubos varias veces. En La casa que construyó Teale (1940), describió una casa construida como un desarrollo de un tesseract y luego, debido a un terremoto, se "formó" en la cuarta dimensión y se convirtió en un tesseract "real". La novela Road of Glory de Heinlein describe una caja de gran tamaño que era más grande por dentro que por fuera.

La historia de Henry Kuttner "All tenals of the Borogov" describe un juguete educativo para niños del futuro lejano, similar en estructura a un tesseract.

Cube 2: Hypercube se centra en ocho extraños atrapados en un hipercubo o red de cubos interconectados.

Mundo paralelo

Las abstracciones matemáticas dieron lugar a la idea de la existencia de mundos paralelos. Éstas se entienden como realidades que existen simultáneamente con la nuestra, pero independientemente de ella. Un mundo paralelo puede ser de varios tamaños, desde un área geográfica pequeña hasta un universo entero. En un mundo paralelo, los eventos ocurren a su manera, puede diferir de nuestro mundo, tanto en detalles individuales como en casi todo. Además, las leyes físicas de un mundo paralelo no son necesariamente análogas a las leyes de nuestro Universo.

Este tema es un terreno fértil para los escritores de ciencia ficción.

La pintura de Salvador Dali "Crucifixión" representa un tesseract. "Crucifixión o cuerpo hipercúbico" - una pintura del artista español Salvador Dalí, pintado en 1954. Representa a Jesucristo crucificado en un escaneo de tesseract. La pintura se conserva en el Museo Metropolitano de Arte de Nueva York.

Todo comenzó en 1895, cuando Herbert Wells reveló la existencia de mundos paralelos para la fantasía con su cuento "Una puerta en una pared". En 1923, Wells volvió a la idea de los mundos paralelos y colocó en uno de ellos un país utópico, donde van los personajes de la novela People as Gods.

La novela no pasó desapercibida. En 1926, apareció la historia de G. Dent "El Emperador del País" Si ". En la historia de Dent, por primera vez, surgió la idea de que podría haber países (mundos) cuya historia podría ser diferente a la historia de los países reales. en nuestro mundo, estos no son menos reales que el nuestro.

En 1944, Jorge Luis Borges publicó el cuento El jardín de senderos que se bifurcan en su libro Cuentos de ficción. Aquí, la idea de la ramificación del tiempo se expresó finalmente con la mayor claridad.
A pesar de la aparición de las obras enumeradas anteriormente, la idea de muchos mundos comenzó a desarrollarse seriamente en la ciencia ficción solo a fines de los años cuarenta del siglo XX, aproximadamente al mismo tiempo que surgió una idea similar en la física.

Uno de los pioneros de una nueva dirección en la ciencia ficción fue John Bixby, quien sugirió en su historia "One-Way Street" (1954) que entre mundos solo puedes moverte en una dirección: habiendo pasado de tu mundo a uno paralelo, no volverás, sino que pasarás de un mundo a otro. Sin embargo, tampoco se excluye el regreso al propio mundo; para ello, es necesario que el sistema de mundos esté cerrado.

La novela de Clifford Simak "Un anillo alrededor del sol" (1982) describe numerosos planetas de la Tierra, cada uno existente en su propio mundo, pero en la misma órbita, y estos mundos y estos planetas difieren entre sí solo por un ligero (microsegundo) cambio en el tiempo ... Las numerosas tierras visitadas por el héroe de la novela forman un único sistema de mundos.

Alfred Bester expresó una mirada interesante a la ramificación de mundos en la historia "El hombre que mató a Mohammed" (1958). "Cambiando el pasado", argumentó el héroe de la historia, "lo cambias solo por ti mismo". En otras palabras, después de un cambio en el pasado, surge una rama de la historia, en la que este cambio existe solo para el personaje que hizo el cambio.

La historia de los hermanos Strugatsky "El lunes comienza el sábado" (1962) describe los viajes de personajes en diferentes versiones del futuro descritos por escritores de ciencia ficción, en contraste con los viajes que ya existían en la ciencia ficción a diferentes versiones del pasado.

Sin embargo, incluso una simple lista de todas las obras en las que se aborda el tema de los mundos paralelos llevaría demasiado tiempo. Y aunque los escritores de ciencia ficción, por regla general, no sustentan científicamente el postulado de la multidimensionalidad, tienen razón en una cosa: esta es una hipótesis que tiene derecho a existir.
La cuarta dimensión del tesseract todavía nos espera.

Victor Savinov

Si eres fanático de las películas de Los Vengadores, lo primero que te viene a la mente cuando escuchas la palabra "Tesseract" es el recipiente transparente en forma de cubo de la Piedra del Infinito que contiene un poder ilimitado.

Para los fanáticos del Universo Marvel, el Tesseract es un cubo azul brillante que hace que las personas no solo de la Tierra, sino también de otros planetas se vuelvan locas. Es por eso que todos los Vengadores se han unido para proteger a los terrícolas de las fuerzas extremadamente destructivas del Tesseract.

Sin embargo, hay que decir lo siguiente: El Tesseract es un concepto geométrico real, o más bien, una forma que existe en 4D. Esto no es solo un cubo azul de los Vengadores ... es un concepto real.

El Tesseract es un objeto en 4 dimensiones. Pero antes de explicarlo en detalle, comencemos desde el principio.

¿Qué es la dimensión?

Todo el mundo ha escuchado los términos 2D y 3D, que representan respectivamente objetos bidimensionales o tridimensionales en el espacio. Pero, ¿qué son estos?

La medición es simplemente la dirección en la que puede ir. Por ejemplo, si está dibujando una línea en una hoja de papel, puede ir hacia la izquierda / derecha (eje x) o hacia arriba / abajo (eje y). Así, decimos que el papel es bidimensional, ya que solo se puede caminar en dos direcciones.

Hay una sensación de profundidad en 3D.

Ahora, en el mundo real, además de las dos direcciones mencionadas anteriormente (izquierda / derecha y arriba / abajo), también puede ir hacia / desde. Por lo tanto, se agrega una sensación de profundidad en el espacio 3D. Por tanto, decimos que la vida real es tridimensional.

Un punto puede representar 0 dimensiones (ya que no se mueve en ninguna dirección), una línea representa 1 dimensión (largo), un cuadrado representa 2 dimensiones (largo y ancho) y un cubo representa 3 dimensiones (largo, ancho y alto ).

Tome un cubo 3D y reemplace cada cara (que actualmente es un cuadrado) con un cubo. ¡Y entonces! La forma que obtienes es el tesseract.

¿Qué es un tesseract?

En pocas palabras, un tesseract es un cubo en un espacio de 4 dimensiones. También se puede decir que es un análogo 4D de un cubo. Es una forma 4D donde cada cara es un cubo.

Proyección 3D de un tesseract que gira dos veces alrededor de dos planos ortogonales.
Imagen: Jason Hise

He aquí una forma sencilla de conceptualizar las dimensiones: un cuadrado es bidimensional; por lo tanto, cada una de sus esquinas tiene 2 líneas que se extienden desde ella en un ángulo de 90 grados entre sí. El cubo es 3D, por lo que cada una de sus esquinas tiene 3 líneas que descienden de él. Del mismo modo, el tesseract tiene forma de 4D, por lo que cada esquina tiene 4 líneas que se extienden desde él.

¿Por qué es difícil imaginar un tesseract?

Dado que nosotros, como seres humanos, hemos evolucionado para visualizar objetos en tres dimensiones, cualquier cosa que entre en dimensiones adicionales como 4D, 5D, 6D, etc., no tiene mucho sentido para nosotros, porque no podemos tenerlos en absoluto. Nuestro cerebro no puede comprender la cuarta dimensión en el espacio. Simplemente no podemos pensar en eso.

Puntos (± 1, ± 1, ± 1, ± 1). En otras palabras, se puede representar como el siguiente conjunto:

El tesseract está delimitado por ocho hiperplanos, cuya intersección con el propio tesseract define sus caras tridimensionales (que son cubos ordinarios). Cada par de caras 3D no paralelas se cruzan para formar caras 2D (cuadrados), y así sucesivamente. Finalmente, un tesseract tiene 8 caras 3D, 24 2D, 32 aristas y 16 vértices.

Descripción popular

Intentemos imaginar cómo se verá el hipercubo sin dejar un espacio tridimensional.

En un "espacio" unidimensional - en una línea - seleccione un segmento AB de longitud L. En un plano bidimensional a una distancia L de AB, dibuje un segmento DC paralelo a él y conecte sus extremos. El resultado es un CDBA cuadrado. Repitiendo esta operación con el plano, obtenemos un cubo tridimensional CDBAGHFE. Y desplazando el cubo en la cuarta dimensión (perpendicular a las tres primeras) en una distancia L, obtenemos el hipercubo CDBAGHFEKLJIOPNM.

Construyendo un tesseract en un avión

El segmento unidimensional AB es el lado del cuadrado bidimensional CDBA, el cuadrado es el lado del cubo CDBAGHFE, que, a su vez, será el lado del hipercubo tetradimensional. Un segmento de línea recta tiene dos puntos límite, un cuadrado tiene cuatro vértices y un cubo tiene ocho. Así, en un hipercubo de cuatro dimensiones, habrá 16 vértices: 8 vértices del cubo original y 8 desplazados en la cuarta dimensión. Tiene 32 aristas - 12 de cada una dan la posición inicial y final del cubo original, y 8 aristas más "dibujarán" sus ocho vértices, que se han movido a la cuarta dimensión. Se puede hacer el mismo razonamiento para las caras del hipercubo. En el espacio bidimensional, es uno (el cuadrado en sí), el cubo tiene 6 de ellos (dos caras del cuadrado movido y cuatro más describirán sus lados). Un hipercubo de cuatro dimensiones tiene 24 caras cuadradas: 12 cuadrados del cubo original en dos posiciones y 12 cuadrados de sus doce bordes.

Como los lados de un cuadrado son 4 segmentos unidimensionales y los lados (caras) de un cubo son 6 cuadrados bidimensionales, para un "cubo de cuatro dimensiones" (tesseract), los lados son 8 cubos tridimensionales . Los espacios de pares opuestos de cubos tesseract (es decir, los espacios tridimensionales a los que pertenecen estos cubos) son paralelos. En la figura, estos son cubos: CDBAGHFE y KLJIOPNM, CDBAKLJI y GHFEOPNM, EFBAMNJI y GHDCOPLK, CKIAGOME y DLJBHPNF.

De manera similar, podemos continuar el razonamiento para hipercubos de un mayor número de dimensiones, pero es mucho más interesante ver cómo se verá un hipercubo de cuatro dimensiones para nosotros, habitantes del espacio tridimensional. Usemos el conocido método de analogía para esto.

Tome un cubo de alambre ABCDHEFG y mírelo con un ojo desde el costado de la cara. Veremos y podemos dibujar dos cuadrados en el plano (sus caras cercanas y lejanas), conectadas por cuatro líneas: bordes laterales. De manera similar, un hipercubo de cuatro dimensiones en un espacio tridimensional se verá como dos "cajas" cúbicas insertadas entre sí y conectadas por ocho bordes. En este caso, las "cajas" en sí mismas, caras tridimensionales, se proyectarán en "nuestro" espacio, y las líneas que las conectan se estirarán en la dirección del cuarto eje. También puede intentar imaginar un cubo no en proyección, sino en una imagen espacial.

Así como un cubo tridimensional está formado por un cuadrado desplazado por la longitud de una cara, un cubo desplazado a la cuarta dimensión formará un hipercubo. Está limitado por ocho cubos, que en perspectiva parecerán una figura bastante compleja. El mismo hipercubo de cuatro dimensiones consta de un número infinito de cubos, al igual que un cubo de tres dimensiones se puede "cortar" en un número infinito de cuadrados planos.

Después de cortar seis caras de un cubo tridimensional, puede expandirlo a una forma plana: un barrido. Tendrá un cuadrado a cada lado de la cara original más uno más, la cara opuesta. Y el despliegue tridimensional del hipercubo de cuatro dimensiones consistirá en el cubo original, seis cubos "creciendo" de él, más uno más: la "hipercara" final.

Las propiedades de Tesseract son la continuación de las propiedades de figuras geométricas de dimensiones inferiores en un espacio de cuatro dimensiones.

Proyección

En el espacio bidimensional

Esta estructura es difícil para la imaginación, pero es posible proyectar un tesseract en espacios 2D o 3D. Además, la proyección al plano facilita la comprensión de la ubicación de los vértices del hipercubo. De esta forma, se pueden obtener imágenes que ya no reflejan relaciones espaciales dentro del tesseract, pero que ilustran la estructura de las conexiones de vértices, como en los siguientes ejemplos:

La tercera imagen muestra el tesseract en vista isométrica, en relación con el punto de construcción. Esta vista es de interés cuando se usa un tesseract como base para una red topológica para vincular múltiples procesadores en computación en paralelo.

En el espacio tridimensional

Una de las proyecciones del tesseract en el espacio tridimensional está representada por dos cubos tridimensionales anidados, cuyos vértices correspondientes están conectados por segmentos. Los cubos internos y externos tienen diferentes tamaños en el espacio tridimensional, pero en el espacio tetradimensional son cubos iguales. Para comprender la igualdad de todos los cubos del tesseract, se creó un modelo de tesseract rotatorio.

• Las seis pirámides truncadas en los bordes del tesseract son imágenes de seis cubos iguales. Sin embargo, estos cubos son como un teseracto, como cuadrados (caras) de un cubo. Pero, de hecho, el tesseract se puede dividir en un número infinito de cubos, como un cubo, en un número infinito de cuadrados, o un cuadrado, en un número infinito de segmentos.

Otra proyección interesante del tesseract en el espacio tridimensional es un dodecaedro rómbico con sus cuatro diagonales dibujadas, conectando pares de vértices opuestos en grandes ángulos de rombos. En este caso, 14 de los 16 vértices del tesseract se proyectan en 14 vértices del rombododecaedro, y las proyecciones de los 2 restantes coinciden en su centro. En tal proyección en un espacio tridimensional, se preservan la igualdad y el paralelismo de todos los lados unidimensionales, bidimensionales y tridimensionales.

Par estéreo

Un estereopar de un tesseract se representa como dos proyecciones en un espacio tridimensional. Esta imagen de tesseract fue diseñada para representar la profundidad como una cuarta dimensión. Se visualiza un estereopar de modo que cada ojo ve solo una de estas imágenes, aparece una imagen estereoscópica que reproduce la profundidad del tesseract.

Desdoblando el tesseract

La superficie de un tesseract se puede expandir en ocho cubos (similar a cómo la superficie de un cubo se puede expandir en seis cuadrados). Hay 261 tesseract desplegados diferentes. El despliegue del tesseract se puede calcular dibujando esquinas conectadas en el gráfico.

Tesseract en el arte

• En New Abbott Plains de Edwine A., el hipercubo es el narrador.
• En un episodio de Las aventuras de Jimmy Neutron, el "chico genio" Jimmy inventa un hipercubo de cuatro dimensiones idéntico al cuadro plegable de El camino a la gloria (1963) de Robert Heinlein.
• Robert E. Heinlein ha mencionado los hipercubos en al menos tres historias de ciencia ficción. En "La casa de las cuatro dimensiones" ("La casa que construyó Teal"), describió una casa construida como un desarrollo de un tesseract, y luego, debido a un terremoto, "se formó" en la cuarta dimensión y se convirtió en un "real "tesseract.
• La novela Road of Glory de Heinlein describe una caja de gran tamaño que era más grande por dentro que por fuera.
• La historia de Henry Kuttner "All tenals of the Borogov" describe un juguete educativo para niños del futuro lejano, similar en estructura a un tesseract.
• En la novela de Alex Garland (), el término "tesseract" se usa para un despliegue tridimensional de un hipercubo de cuatro dimensiones, en lugar del hipercubo en sí. Ésta es una metáfora diseñada para mostrar que el sistema cognitivo debería ser más amplio que el reconocible.
• Cube 2: Hypercube se centra en ocho extraños atrapados en un hipercubo o red de cubos interconectados.
• La serie de televisión Andromeda usa generadores de tesseract como un dispositivo de conspiración. Están diseñados principalmente para manipular el espacio y el tiempo.
• Cuadro "Crucifixión" (Corpus Hypercubus) de Salvador Dali ().
• El cómic Nextwave muestra un vehículo que incluye 5 zonas de tesseract.
• En el álbum Nothingface de Voivod, una de las canciones se llama "In my hypercube".
• En la novela de Anthony Pierce "Ruta Cuba" una de las lunas en órbita de la Asociación Internacional de Fomento se llama tesseract, que se comprimió en 3 dimensiones.
• En la serie "Escuela" Agujero negro "" en la tercera temporada hay una serie "Tesseract". Lucas presiona un botón secreto y la escuela comienza a "tomar forma como un tesseract matemático".
• El término "tesseract" y el término "tesserate", derivado de él, se encuentran en la historia de Madeleine L'Engle "The Fold of Time".
• TesseracT es el nombre de un grupo de caballeros británicos.
• En la serie de películas Marvel Cinematic Universe, el Tesseract es un elemento clave de la trama, un artefacto espacial con forma de hipercubo.
• En la historia de Robert Sheckley "Miss Mouse y la Cuarta Dimensión", un escritor esotérico, un conocido del autor, intenta ver un teseracto, buscando durante horas un dispositivo que ha construido: una bola en un vástago con varillas clavadas, en el que se plantan cubos, pegados con todos los símbolos esotéricos. La historia menciona el trabajo de Hinton.
• En las películas Capitán América: Los Vengadores. Tesseract-energía de todo el universo

Otros nombres

• Hexadekahoron (ing. Hexadecacoron)
• Octohoron (ing. Octachoron)
• Tetracubus
• 4 cubos
• Hipercubo (si no se especifica el número de medidas)

Notas (editar)

Literatura

• Charles H. Hinton. Cuarta dimensión, 1904. ISBN 0-405-07953-2
• Martin Gardner, Mathmatical Carnival, 1977. ISBN 0-394-72349-X
• Ian Stewart, Conceptos de matemáticas modernas, 1995. ISBN 0-486-28424-7

Enlaces

En ruso

• Programa Transformator4D. Formación de modelos de proyecciones tridimensionales de objetos de cuatro dimensiones (incluido el Hipercubo).
• Un programa que implementa la construcción de un tesseract y todas sus transformaciones afines, con fuentes en C ++.

En Inglés

• Mushware Limited - Programa de inferencia Tesseract ( Entrenador Tesseract, licencia compatible con GPLv2) y juego de disparos en primera persona en un espacio de cuatro dimensiones ( Adanaxis; gráficos, en su mayoría tridimensionales; hay una versión bajo la GPL en los repositorios del SO).

Poliedros
Correcto (Sólidos platónicos)
Dodecaedro estrellado Iicosidodecaedro estrellado Iicosaedro estrellado Poliedro estrellado Octaedro estrellado
Convexo	Cuerpos de Arquímedes Cuboctaedro Icosidodecaedro Tetraedro truncado Octaedro truncado Iicosaedro anti-truncado Cubo truncado Dodecaedro truncado Rombocuboctaedro Romboicosododecaedro Cuboctaedro rombo truncado Cuboctaedro rombo truncado Cuboctaedro rombo truncado Dodecaedro truncado Truncado Cuerpos Catalanes Rombododecaedro Rombotriacontaedro Triakistetraedro Tetrakishexaedro Pentakisdodecaedro Triakisoktaedro Triakisycosaedro Iicositetraedro deltoidal Hexcontaedro deltoidal Icostetraedro pentagonal Sin simetría espacial completa Pirámide Prisma Bipirámide Antiprisma Zonoedro Paralelepípedo Romboedro Prismatoide Pirámide truncada Pentagondodecaedro paraleloedro
Fórmulas, teoremas, teoría
Otro

Hipercubo y sólidos platónicos

Simular un icosaedro truncado ("balón de fútbol") en el sistema "Vector"
en el que cada pentágono está delimitado por hexágonos

Icosaedro truncado se puede obtener cortando 12 vértices con la formación de caras en forma de pentágonos regulares. En este caso, el número de vértices del nuevo poliedro aumenta 5 veces (12 × 5 = 60), 20 caras triangulares se convierten en hexágonos regulares (en total caras se vuelven 20 + 12 = 32), a el número de aristas aumenta a 30 + 12 × 5 = 90.

Pasos para construir un icosaedro truncado en el sistema "Vector"

Formas en un espacio de 4 dimensiones.

--à

--à ?

Por ejemplo, dado un cubo y un hipercubo. Hay 24 caras en un hipercubo. Esto significa que un octaedro de 4 dimensiones tendrá 24 vértices. Aunque no, un hipercubo tiene 8 caras de cubos, cada uno tiene un vértice central. Esto significa que un octaedro de 4 dimensiones tendrá 8 vértices que son más fáciles.

Octaedro de 4 dimensiones... Consiste en ocho tetraedros equiláteros e iguales,
conectados por cuatro en cada vértice.

Arroz. Intenta simular
hiperesfera-hiperesfera en el sistema "Vector"

Anverso - reverso - bolas sin distorsión. Seis bolas más: puede especificar mediante elipsoides o superficies cuadráticas (mediante 4 líneas de contorno como generadores) o mediante caras (primero especificado mediante generadores).

Más trucos para "construir" una hiperesfera
- el mismo "balón de fútbol" en un espacio de 4 dimensiones

Apéndice 2

Para los poliedros convexos, existe una propiedad que conecta el número de sus vértices, aristas y caras, probada en 1752 por Leonard Euler y llamada teorema de Euler.

Antes de formularlo, considere los poliedros que conocemos y complete la siguiente tabla, en la que B es el número de vértices, P son las aristas y G son las caras de un politopo dado:

Nombre del poliedro
Pirámide triangular
Pirámide cuadrangular
Prisma triangular
Prisma cuadrangular
n -pirámide de carbón	norte+1	2norte	norte+1
n -prisma de carbono	2norte	3norte	n + 2
n -carbón truncado pirámide	2norte	3norte	n + 2

De esta tabla podemos ver directamente que para todos los politopos seleccionados se cumple la igualdad B - P + Γ = 2. Resulta que esta igualdad es válida no solo para estos poliedros, sino también para un poliedro convexo arbitrario.

Teorema de Euler. Para cualquier politopo convexo, la igualdad

B - R + G = 2,

donde B es el número de vértices, P es el número de aristas y G es el número de caras de un poliedro dado.

Prueba. Para demostrar esta igualdad, representamos la superficie de un poliedro dado hecho de un material elástico. Eliminemos (recortemos) una de sus caras y estiremos la superficie restante en un plano. Obtenemos un polígono (formado por los bordes de la cara distante del poliedro), dividido en polígonos más pequeños (formado por las otras caras del poliedro).

Tenga en cuenta que los polígonos pueden deformarse, agrandarse, reducirse o incluso curvarse en sus lados, siempre que los lados no se rompan. Esto no cambia el número de vértices, aristas y caras.

Demostremos que para la partición resultante de un polígono en polígonos más pequeños, se cumple la siguiente igualdad:

(*) B - R + G "= 1,

donde В es el número total de vértices, Р es el número total de aristas y Г "es el número de polígonos incluidos en la partición. Está claro que Г" = Г - 1, donde Г es el número de caras de un determinado poliedro.

Demostremos que la igualdad (*) no cambia si se dibuja una diagonal en algún polígono de la partición dada (Fig. 5, a). De hecho, después de dibujar dicha diagonal en la nueva partición, habrá vértices B, bordes P + 1 y el número de polígonos aumentará en uno. Por lo tanto, tenemos

B - (P + 1) + (G "+1) = B - P + G" .

Usando esta propiedad, dibujamos diagonales dividiendo los polígonos entrantes en triángulos, y para la partición resultante mostramos que se cumple la igualdad (*) (Fig. 5, b). Para hacer esto, eliminaremos constantemente los bordes exteriores, reduciendo el número de triángulos. En este caso, son posibles dos casos:

a) quitar el triangulo A B C se requiere quitar dos costillas, en nuestro caso AB y antes de Cristo;

b) quitar el trianguloMKNse requiere quitar un borde, en nuestro casoMinnesota.

En ambos casos, la igualdad (*) no cambiará. Por ejemplo, en el primer caso, después de eliminar el triángulo, el gráfico constará de B - 1 vértices, P - 2 aristas y G "- 1 polígono:

(B - 1) - (R + 2) + (G "- 1) = B - R + G".

Considere el segundo caso por su cuenta.

Por lo tanto, eliminar un triángulo no cambia la igualdad (*). Continuando con este proceso de borrar triángulos, al final llegamos a una partición que consta de un triángulo. Para tal partición, B = 3, P = 3, Γ "= 1 y, por lo tanto, B - P + Γ" = 1. Por lo tanto, la igualdad (*) también es válida para la partición original, de donde finalmente obtenemos que para un dada la partición del polígono, la igualdad (*) es verdadera. Por lo tanto, para el politopo convexo original, la igualdad B - P + Γ = 2 es verdadera.

Un ejemplo de un poliedro para el que no se cumple la relación de Euler, se muestra en la Figura 6. Este poliedro tiene 16 vértices, 32 aristas y 16 caras. Por lo tanto, para este poliedro, se cumple la igualdad B - P + Γ = 0.

Apéndice 3.

Film Cube 2: Hypercube "(ing. Cube 2: Hypercube) - una película fantástica, la continuación de la película" Cube ".

Ocho desconocidos se despiertan en habitaciones en forma de cubo. Las habitaciones están ubicadas dentro de un hipercubo de cuatro dimensiones. Las habitaciones se mueven constantemente por "teletransportación cuántica", y si subes a la siguiente habitación, es poco probable que vuelvas a la antigua. En un hipercubo, los mundos paralelos se cruzan, el tiempo fluye en algunas habitaciones de diferentes maneras y algunas habitaciones son trampas mortales.

La trama de la imagen repite en gran medida la historia de la primera parte, que también se refleja en las imágenes de algunos de los personajes. El premio Nobel Rosenzweig, que calculó la hora exacta de la destrucción del hipercubo, muere en las habitaciones del hipercubo.

Crítica

Si en la primera parte las personas encarceladas en un laberinto intentaron ayudarse entre sí, en esta película es cada uno por sí mismo. Hay muchos efectos especiales innecesarios (son trampas) que no conectan lógicamente esta parte de la película con la anterior. Es decir, resulta que la película Cube 2: esta es una especie de laberinto del futuro 2020-2030, pero no 2000. En la primera parte, teóricamente una persona puede crear todo tipo de trampas. En la segunda parte, estas trampas son un programa informático, el llamado "Realidad Virtual".