टेसेरैक्ट क्या है? साइबरक्यूब - चौथा आयाम त्रि-आयामी वर्ग में पहला कदम।

29.08.2021 बगीचे में तालाब

ज्यामिति में अतिविम- यह है एनवर्ग की -आयामी सादृश्य ( एन= 2) और घन ( एन= 3)। यह एक बंद, उत्तल आकृति है, जो आकृति के विपरीत किनारों पर स्थित समानांतर रेखाओं के समूहों से बनी होती है, और एक दूसरे से समकोण पर जुड़ी होती है।

इस आंकड़े को . के रूप में भी जाना जाता है टेसेरैक्ट(टेसरैक्ट)। टेसेरैक्ट एक क्यूब को संदर्भित करता है क्योंकि क्यूब एक वर्ग को संदर्भित करता है। अधिक औपचारिक रूप से, एक टेस्सेक्ट को एक नियमित उत्तल चार-आयामी पॉलीटोप (पॉलीटोप) के रूप में वर्णित किया जा सकता है, जिसकी सीमा में आठ घन कोशिकाएं होती हैं।

ऑक्सफोर्ड इंग्लिश डिक्शनरी के अनुसार, टेसेरैक्ट शब्द 1888 में चार्ल्स हॉवर्ड हिंटन द्वारा गढ़ा गया था और अपनी पुस्तक ए न्यू एरा ऑफ थॉट में इस्तेमाल किया गया था। शब्द ग्रीक "τεσσερες ακτινες" ("चार किरण") से बना था, निर्देशांक के चार अक्ष हैं। इसके अलावा, कुछ स्रोतों में, एक ही आंकड़ा कहा जाता था टेट्राक्यूब(टेट्राक्यूब)।

एन-आयामी हाइपरक्यूब को भी कहा जाता है एन-घन.

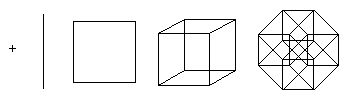
एक बिंदु आयाम 0 का एक हाइपरक्यूब है। यदि आप लंबाई की एक इकाई द्वारा एक बिंदु को स्थानांतरित करते हैं, तो आपको इकाई लंबाई का एक खंड मिलता है - आयाम का एक हाइपरक्यूब। इसके अलावा, यदि आप लंबाई की एक इकाई द्वारा एक खंड को लंबवत दिशा में ले जाते हैं। खंड की दिशा में, आपको एक घन मिलता है - आयाम का एक हाइपरक्यूब 2. वर्ग के विमान के लंबवत दिशा में लंबाई की एक इकाई द्वारा एक वर्ग को स्थानांतरित करने पर, एक घन प्राप्त होता है - आयाम का एक हाइपरक्यूब 3. यह प्रक्रिया किसी भी आयाम के लिए सामान्यीकृत किया जा सकता है। उदाहरण के लिए, यदि आप चौथे आयाम में एक घन को लंबाई की एक इकाई ले जाते हैं, तो आपको एक टेसेरैक्ट मिलता है।

हाइपरक्यूब्स का परिवार कुछ नियमित पॉलीहेड्रा में से एक है जिसे किसी भी आयाम में दर्शाया जा सकता है।

हाइपरक्यूब तत्व

आयाम हाइपरक्यूब एन 2 . है एन"पक्ष" (एक-आयामी रेखा में 2 बिंदु होते हैं; द्वि-आयामी वर्ग - 4 भुजाएँ; त्रि-आयामी घन - 6 फलक; चार-आयामी टेसरैक्ट - 8 कोशिकाएँ)। हाइपरक्यूब के शीर्षों (बिंदुओं) की संख्या 2 . है एन(उदाहरण के लिए, घन के लिए - 2 3 कोने)।

मात्रा एम-सीमा पर आयामी हाइपरक्यूब एन-घन बराबर

उदाहरण के लिए, एक हाइपरक्यूब की सीमा में 8 घन, 24 वर्ग, 32 किनारे और 16 शीर्ष होते हैं।

हाइपरक्यूब के तत्व

एन-घन	नाम	शिखर (0-किनारे)	किनारा (1-पक्ष)	किनारा (2-पक्ष)	कक्ष (3-पक्ष)	(4-पक्ष)	(5-पक्ष)	(6-पक्ष)	(7-पक्ष)	(8-पक्ष)
0-घन	बिंदु	1
1-घन	अनुभाग	2	1
2-घन	वर्ग	4	4	1
3-क्यूब	घनक्षेत्र	8	12	6	1
4-घन	टेसेरैक्ट	16	32	24	8	1
5-क्यूब	पेंटरक्तो	32	80	80	40	10	1
6-घन	हेक्सरैक्ट	64	192	240	160	60	12	1
7-घन	हेप्टरैक्ट	128	448	672	560	280	84	14	1
8-घन	ऑक्ट्रैक्ट	256	1024	1792	1792	1120	448	112	16	1
9-घन	Eneneract	512	2304	4608	5376	4032	2016	672	144	18

विमान प्रक्षेपण

हाइपरक्यूब के गठन को निम्नलिखित तरीके से दर्शाया जा सकता है:

दो बिंदुओं A और B को एक रेखाखंड AB बनाने के लिए जोड़ा जा सकता है।
एक वर्ग ABCD बनाने के लिए दो समानांतर रेखाखंड AB और CD को जोड़ा जा सकता है।
दो समानांतर वर्ग ABCD और EFGH को एक घन ABCDEFGH बनाने के लिए जोड़ा जा सकता है।
दो समानांतर घन ABCDEFGH और IJKLMNOP को हाइपरक्यूब ABCDEFGHIJKLMNOP बनाने के लिए जोड़ा जा सकता है।

बाद की संरचना की कल्पना करना आसान नहीं है, लेकिन इसके प्रक्षेपण को 2D या 3D स्थान पर चित्रित करना संभव है। इसके अलावा, अनुमानित शिखर की स्थिति को पुनर्व्यवस्थित करने में सक्षम होने के कारण 2 डी विमान पर अनुमान अधिक उपयोगी हो सकते हैं। इस मामले में, छवियां प्राप्त की जा सकती हैं जो अब टेसरैक्ट के भीतर तत्वों के स्थानिक संबंधों को प्रतिबिंबित नहीं करती हैं, लेकिन नीचे दिए गए उदाहरणों में शीर्ष कनेक्शन की संरचना का वर्णन करती हैं।

पहला दृष्टांत दिखाता है कि कैसे, सिद्धांत रूप में, दो घनों को मिलाकर एक टेस्सेक्ट का निर्माण किया जाता है। यह आरेख दो-वर्ग घन बनाने के आरेख के समान है। दूसरे आरेख से पता चलता है कि टेस्सेक्ट के सभी किनारों की लंबाई समान है। यह योजना आपको एक दूसरे से जुड़े घनों को खोजने के लिए भी बाध्य करती है। तीसरे आरेख में, टेसरैक्ट के कोने नीचे के बिंदु के सापेक्ष किनारों के साथ दूरियों के अनुसार स्थित हैं। यह योजना इस मायने में दिलचस्प है कि समानांतर कंप्यूटिंग का आयोजन करते समय इसे कनेक्टिंग प्रोसेसर के नेटवर्क टोपोलॉजी के लिए एक बुनियादी योजना के रूप में उपयोग किया जाता है: किसी भी दो नोड्स के बीच की दूरी 4 किनारे की लंबाई से अधिक नहीं होती है, और लोड को संतुलित करने के कई अलग-अलग तरीके हैं।

कला में हाइपरक्यूब

हाइपरक्यूब 1940 से विज्ञान कथा साहित्य में दिखाई दिया है, जब रॉबर्ट हेनलेन ने अपनी कहानी "एंड ही बिल्ट ए क्रुक्ड हाउस" में एक टेसेरैक्ट स्वीप के आकार में बने घर का वर्णन किया था। कहानी में, यह आगे, यह घर ढह जाता है, एक चार-आयामी टेसरेक्ट में बदल जाता है। उसके बाद, कई किताबों और उपन्यासों में हाइपरक्यूब दिखाई देता है।

फिल्म "क्यूब 2: हाइपरक्यूब" हाइपरक्यूब के नेटवर्क में फंसे आठ लोगों की कहानी कहती है।

साल्वाडोर डाली की पेंटिंग "क्रूसीफिक्सियन" ("क्रूसीफिक्सियन (कॉर्पस हाइपरक्यूबस)", 1954) में यीशु को टेसेरैक्ट स्कैन पर सूली पर चढ़ाते हुए दिखाया गया है। यह पेंटिंग न्यूयॉर्क में मेट्रोपॉलिटन म्यूजियम ऑफ आर्ट में देखी जा सकती है।

निष्कर्ष

हाइपरक्यूब सबसे सरल चार-आयामी वस्तुओं में से एक है, जिसके उदाहरण से आप चौथे आयाम की सभी जटिलता और असामान्यता देख सकते हैं। और जो तीन आयामों में असंभव दिखता है, शायद चार में, उदाहरण के लिए, असंभव आंकड़े। इसलिए, उदाहरण के लिए, चार आयामों में एक असंभव त्रिभुज की सलाखों को समकोण पर जोड़ा जाएगा। और यह आंकड़ा सभी दृष्टिकोणों से इस तरह दिखेगा, और विकृत नहीं होगा, त्रि-आयामी अंतरिक्ष में असंभव त्रिभुज की प्राप्ति के विपरीत (देखें।

यदि आपके साथ कोई असामान्य घटना घटी हो, आपने कोई अजीब प्राणी देखा हो या कोई समझ से परे घटना हो, आपने एक असामान्य सपना देखा हो, आपने आकाश में एक UFO देखा हो या किसी विदेशी अपहरण का शिकार हुआ हो, आप हमें अपनी कहानी भेज सकते हैं और यह होगी हमारी वेबसाइट पर प्रकाशित ===> .

बहुआयामी रिक्त स्थान का सिद्धांत 19वीं शताब्दी के मध्य में प्रकट होने लगा। वैज्ञानिकों ने चार आयामी अंतरिक्ष का विचार वैज्ञानिकों से लिया है। उन्होंने अपने कार्यों में चौथे आयाम के अद्भुत चमत्कारों के बारे में दुनिया को बताया।

उनके कार्यों के नायक, चार-आयामी अंतरिक्ष के गुणों का उपयोग करते हुए, अंडे की सामग्री को खोल को नुकसान पहुंचाए बिना खा सकते थे, बोतल कैप को खोले बिना एक पेय पी सकते थे। चौथे आयाम से चोरों ने तिजोरी से खजाना बरामद किया। सर्जन ने मरीज के शरीर के ऊतकों को काटे बिना आंतरिक अंगों का ऑपरेशन किया।

टेसेरैक्ट

ज्यामिति में, एक हाइपरक्यूब एक वर्ग (एन = 2) और एक घन (एन = 3) का एक एन-आयामी सादृश्य है। हमारे सामान्य त्रि-आयामी घन के चार-आयामी एनालॉग को टेसेरैक्ट के रूप में जाना जाता है। टेसेरैक्ट एक क्यूब को संदर्भित करता है क्योंकि क्यूब एक वर्ग को संदर्भित करता है। अधिक औपचारिक रूप से, एक टेसेरैक्ट को एक नियमित उत्तल चार-आयामी पॉलीहेड्रॉन के रूप में वर्णित किया जा सकता है जिसकी सीमा में आठ घन कोशिकाएं होती हैं।

गैर-समानांतर 3D चेहरों की प्रत्येक जोड़ी 2D फलक (वर्ग) बनाने के लिए प्रतिच्छेद करती है, और इसी तरह। अंत में, एक टेस्सेक्ट में 8 3D चेहरे, 24 2D, 32 किनारे और 16 कोने होते हैं।
वैसे, ऑक्सफोर्ड डिक्शनरी के अनुसार, 1888 में चार्ल्स हॉवर्ड हिंटन (1853-1907) द्वारा अपनी पुस्तक ए न्यू एज ऑफ थॉट में टेसेरैक्ट को गढ़ा और इस्तेमाल किया गया था। बाद में, कुछ लोगों ने उसी आकृति को टेट्राक्यूबस (ग्रीक टेट्रा - चार) कहा - एक चार-आयामी घन।

निर्माण और विवरण

आइए कल्पना करने की कोशिश करें कि त्रि-आयामी स्थान को छोड़े बिना हाइपरक्यूब कैसा दिखेगा।
एक-आयामी "अंतरिक्ष" में - एक रेखा पर - लंबाई एल के एक खंड एबी का चयन करें। एबी से एल की दूरी पर एक दो-आयामी विमान पर, इसके समानांतर एक खंड डीसी बनाएं और उनके सिरों को जोड़ दें। परिणाम एक वर्ग सीडीबीए है। विमान के साथ इस ऑपरेशन को दोहराते हुए, हमें त्रि-आयामी घन सीडीबीएजीएचई मिलता है। और क्यूब को चौथे आयाम (पहले तीन के लंबवत) में दूरी L से स्थानांतरित करने पर, हमें हाइपरक्यूब CDBAGHFEKLJIOPNM प्राप्त होता है।

इसी तरह, हम बड़ी संख्या में आयामों के हाइपरक्यूब के लिए तर्क जारी रख सकते हैं, लेकिन यह देखना अधिक दिलचस्प है कि त्रि-आयामी अंतरिक्ष के निवासियों, हमारे लिए एक चार-आयामी हाइपरक्यूब कैसा दिखेगा।

एक तार का घन ABCDHEFG लें और इसे चेहरे के किनारे से एक आंख से देखें। हम देखेंगे और चार रेखाओं से जुड़े हुए समतल (इसके निकट और दूर के चेहरे) पर दो वर्ग खींच सकते हैं - किनारे के किनारे। इसी तरह, त्रि-आयामी अंतरिक्ष में एक चार-आयामी हाइपरक्यूब दो क्यूबिक "बक्से" की तरह दिखेगा जो एक दूसरे में डाले गए हैं और आठ किनारों से जुड़े हुए हैं। इस मामले में, "बक्से" स्वयं - त्रि-आयामी चेहरे - "हमारे" स्थान पर प्रक्षेपित किए जाएंगे, और उन्हें जोड़ने वाली रेखाएं चौथे अक्ष की दिशा में फैल जाएंगी। आप प्रक्षेपण में नहीं, बल्कि एक स्थानिक छवि में एक घन की कल्पना करने का प्रयास कर सकते हैं।

जिस तरह एक त्रि-आयामी घन एक चेहरे की लंबाई से स्थानांतरित एक वर्ग द्वारा बनता है, चौथे आयाम में स्थानांतरित एक घन एक हाइपरक्यूब का निर्माण करेगा। यह आठ घनों तक सीमित है, जो परिप्रेक्ष्य में एक जटिल आकृति की तरह दिखाई देगा। उसी चार-आयामी हाइपरक्यूब को अनंत संख्या में क्यूब्स में तोड़ा जा सकता है, जैसे कि एक त्रि-आयामी क्यूब को अनंत संख्या में फ्लैट वर्गों में "काटा" जा सकता है।

त्रि-आयामी घन के छह चेहरों को काटकर, आप इसे एक सपाट आकार में विस्तारित कर सकते हैं - एक झाडू। इसमें मूल चेहरे के प्रत्येक तरफ एक वर्ग होगा और एक और - इसके विपरीत चेहरा। और चार-आयामी हाइपरक्यूब के त्रि-आयामी खुलासा में मूल घन, छह क्यूब्स "बढ़ते" होंगे, साथ ही एक और - अंतिम "हाइपरफेस"।

कला में हाइपरक्यूब

Tesseract इतनी दिलचस्प आकृति है कि इसने बार-बार लेखकों और फिल्म निर्माताओं का ध्यान आकर्षित किया है।
रॉबर्ट ई. हेनलेन ने कई बार हाइपरक्यूब का उल्लेख किया है। द हाउस दैट टीले बिल्ट (1940) में, उन्होंने एक ऐसे घर का वर्णन किया जिसे एक टेसेरैक्ट के विकास के रूप में बनाया गया था, और फिर, एक भूकंप के कारण, चौथे आयाम में "गया" और एक "वास्तविक" टेसरेक्ट बन गया। हेनलेन के उपन्यास रोड ऑफ ग्लोरी में एक बड़े आकार के बॉक्स का वर्णन किया गया है जो बाहर की तुलना में अंदर से बड़ा था।

हेनरी कुट्टनर की कहानी "ऑल टेनल्स ऑफ द बोरोगोव्स" दूर के भविष्य के बच्चों के लिए एक शैक्षिक खिलौने का वर्णन करती है, जो संरचना में एक टेसेरैक्ट के समान है।

घन 2: हाइपरक्यूब एक हाइपरक्यूब, या परस्पर जुड़े घनों के नेटवर्क में फंसे आठ अजनबियों पर ध्यान केंद्रित करता है।

समानांतर विश्व

गणितीय अमूर्तता ने समानांतर दुनिया के अस्तित्व के विचार को जन्म दिया। इन्हें उन वास्तविकताओं के रूप में समझा जाता है जो हमारे साथ एक साथ मौजूद होती हैं, लेकिन इससे स्वतंत्र रूप से। एक छोटे से भौगोलिक क्षेत्र से लेकर पूरे ब्रह्मांड तक एक समानांतर दुनिया विभिन्न आकारों की हो सकती है। समानांतर दुनिया में, घटनाएं अपने तरीके से होती हैं, यह हमारी दुनिया से अलग-अलग विवरण और लगभग हर चीज में भिन्न हो सकती हैं। इसके अलावा, समानांतर दुनिया के भौतिक नियम जरूरी नहीं कि हमारे ब्रह्मांड के नियमों के अनुरूप हों।

यह विषय विज्ञान कथा लेखकों के लिए उपजाऊ जमीन है।

सल्वाडोर डाली की पेंटिंग "क्रूसीफिक्सियन" में एक टेसरेक्ट को दर्शाया गया है। "क्रूसिफिक्सियन या हाइपरक्यूबिक बॉडी" - स्पेनिश कलाकार सल्वाडोर डाली की एक पेंटिंग, जिसे 1954 में चित्रित किया गया था। एक टेसेरैक्ट स्कैन पर सूली पर चढ़ाए गए यीशु मसीह को दर्शाता है। पेंटिंग न्यूयॉर्क में मेट्रोपॉलिटन म्यूज़ियम ऑफ़ आर्ट में है

यह सब 1895 में शुरू हुआ, जब हर्बर्ट वेल्स ने अपनी कहानी "ए डोर इन ए वॉल" के साथ कल्पना के लिए समानांतर दुनिया के अस्तित्व को खोला। 1923 में वेल्स समानांतर दुनिया के विचार पर लौट आए और उनमें से एक में एक यूटोपियन देश रखा, जहां उपन्यास "पीपल एज़ गॉड्स" के पात्रों को भेजा जाता है।

उपन्यास पर किसी का ध्यान नहीं गया। 1926 में, जी. डेंट की कहानी "देश के सम्राट" अगर "प्रकट हुई।" डेंट की कहानी में, पहली बार यह विचार आया कि ऐसे देश (दुनिया) हो सकते हैं जिनका इतिहास वास्तविक देशों के इतिहास से अलग हो सकता है। हमारी दुनिया में ये हमारी तुलना में कम वास्तविक नहीं हैं।

1944 में, जॉर्ज लुइस बोर्गेस ने अपनी पुस्तक फिक्शनल स्टोरीज में कहानी द गार्डन ऑफ फोर्किंग पाथ्स प्रकाशित की। यहाँ समय शाखा के विचार को अंततः अत्यंत स्पष्टता के साथ व्यक्त किया गया था।
ऊपर सूचीबद्ध कार्यों की उपस्थिति के बावजूद, XX सदी के उत्तरार्ध में ही विज्ञान कथाओं में कई-दुनिया के विचार को गंभीरता से विकसित करना शुरू हुआ, लगभग उसी समय जब भौतिकी में एक समान विचार उत्पन्न हुआ था।

विज्ञान कथा में एक नई दिशा के अग्रदूतों में से एक जॉन बिक्सबी थे, जिन्होंने "वन-वे स्ट्रीट" (1954) कहानी में सुझाव दिया था कि दुनिया के बीच आप केवल एक ही दिशा में आगे बढ़ सकते हैं - अपनी दुनिया से समानांतर में जाने के बाद, तुम वापस नहीं जाओगे, लेकिन तुम एक दुनिया से दूसरी दुनिया में चले जाओगे। हालांकि, अपनी खुद की दुनिया में वापसी को भी बाहर नहीं रखा गया है - इसके लिए जरूरी है कि दुनिया की व्यवस्था बंद हो।

क्लिफोर्ड सिमक का उपन्यास "द रिंग अराउंड द सन" (1982) पृथ्वी के कई ग्रहों का वर्णन करता है, जिनमें से प्रत्येक अपनी दुनिया में मौजूद है, लेकिन एक ही कक्षा में है, और ये दुनिया और ये ग्रह एक दूसरे से केवल एक मामूली (एक द्वारा) भिन्न हैं। माइक्रोसेकंड) समय में बदलाव ... उपन्यास के नायक द्वारा देखी गई कई पृथ्वी दुनिया की एक प्रणाली बनाती है।

अल्फ्रेड बेस्टर ने "द मैन हू किल्ड मोहम्मद" (1958) कहानी में दुनिया की शाखाओं पर एक दिलचस्प नज़र डाली। "अतीत को बदलकर," कहानी के नायक ने तर्क दिया, "आप इसे केवल अपने लिए बदल रहे हैं।" दूसरे शब्दों में, अतीत में परिवर्तन के बाद, इतिहास की एक शाखा उत्पन्न होती है, जिसमें यह परिवर्तन केवल उस चरित्र के लिए मौजूद होता है जिसने परिवर्तन किया।

स्ट्रैगात्स्की भाइयों की कहानी "सोमवार शनिवार को शुरू होती है" (1962) विज्ञान कथा लेखकों द्वारा वर्णित भविष्य के विभिन्न संस्करणों में पात्रों की यात्रा का वर्णन करती है - अतीत के विभिन्न संस्करणों के लिए विज्ञान कथा में पहले से मौजूद यात्रा के विपरीत।

हालांकि, समानांतर दुनिया के विषय पर सभी कार्यों की एक साधारण गणना में भी बहुत अधिक समय लगेगा। और यद्यपि विज्ञान कथा लेखक, एक नियम के रूप में, वैज्ञानिक रूप से बहुआयामीता के सिद्धांत की पुष्टि नहीं करते हैं, वे एक बात के बारे में सही हैं - यह एक परिकल्पना है जिसे अस्तित्व का अधिकार है।
टेस्सेक्ट का चौथा आयाम अभी भी हमारा इंतजार कर रहा है।

विक्टर सविनोव

यदि आप एवेंजर्स फिल्मों के प्रशंसक हैं, तो "टेसेरैक्ट" शब्द सुनते ही आपके दिमाग में जो पहली चीज आती है, वह है अनंत शक्ति से युक्त इन्फिनिटी स्टोन का पारदर्शी क्यूब के आकार का बर्तन।

मार्वल यूनिवर्स के प्रशंसकों के लिए, टेसरैक्ट एक चमकता हुआ नीला घन है जो न केवल पृथ्वी, बल्कि अन्य ग्रहों के लोगों को भी दीवाना बना देता है। यही कारण है कि सभी एवेंजर्स ने पृथ्वीवासियों को टेसेरैक्ट की अत्यंत विनाशकारी ताकतों से बचाने के लिए एक साथ बैंड किया है।

हालाँकि, निम्नलिखित कहा जाना चाहिए: Tesseract एक वास्तविक ज्यामितीय अवधारणा है, या यों कहें, एक ऐसा रूप है जो 4D में मौजूद है। यह एवेंजर्स का सिर्फ एक नीला क्यूब नहीं है ... यह एक वास्तविक अवधारणा है।

Tesseract 4 आयामों में एक वस्तु है। लेकिन इससे पहले कि हम इसे विस्तार से समझाएं, आइए शुरुआत से शुरू करते हैं।

आयाम क्या है?

सभी ने 2D और 3D शब्द सुने हैं, जो अंतरिक्ष में क्रमशः द्वि-आयामी या त्रि-आयामी वस्तुओं का प्रतिनिधित्व करते हैं। लेकिन ये क्या हैं?

मापन केवल वह दिशा है जिस पर आप जा सकते हैं। उदाहरण के लिए, यदि आप एक कागज़ के टुकड़े पर एक रेखा खींचते हैं, तो आप बाएँ/दाएँ (x-अक्ष) या ऊपर/नीचे (y-अक्ष) जा सकते हैं। इस प्रकार, हम कहते हैं कि कागज द्वि-आयामी है, क्योंकि आप केवल दो दिशाओं में चल सकते हैं।

3डी में गहराई का अहसास होता है।

अब, वास्तविक दुनिया में, ऊपर वर्णित दो दिशाओं (बाएं / दाएं और ऊपर / नीचे) के अलावा, आप / से भी जा सकते हैं। इसलिए, 3डी स्पेस में गहराई की भावना जुड़ जाती है। इसलिए, हम कहते हैं कि वास्तविक जीवन त्रि-आयामी है।

एक बिंदु 0 आयामों का प्रतिनिधित्व कर सकता है (चूंकि यह किसी भी दिशा में नहीं चलता है), एक रेखा 1 आयाम (लंबाई) का प्रतिनिधित्व करती है, एक वर्ग 2 आयामों (लंबाई और चौड़ाई) का प्रतिनिधित्व करता है, और एक घन 3 आयामों (लंबाई, चौड़ाई और ऊंचाई) का प्रतिनिधित्व करता है। )

एक 3D घन लें और प्रत्येक फलक (जो वर्तमान में एक वर्ग है) को एक घन से बदलें। इसलिए! आपको जो आकार मिलता है वह टेस्सेक्ट है।

एक टेसेरैक्ट क्या है?

सीधे शब्दों में कहें, एक टेस्सेक्ट 4-आयामी अंतरिक्ष में एक घन है। आप यह भी कह सकते हैं कि यह एक क्यूब का 4डी एनालॉग है। यह एक 4D आकार है जहाँ प्रत्येक फलक एक घन है।

टेसरैक्ट का एक 3डी प्रक्षेपण जो दो ओर्थोगोनल विमानों के चारों ओर दो बार घूमता है।
छवि: जेसन हिसे

आयामों की अवधारणा का एक सरल तरीका यहां दिया गया है: एक वर्ग द्वि-आयामी होता है; इसलिए, इसके प्रत्येक कोने में 2 रेखाएँ हैं जो इससे 90 डिग्री के कोण पर एक दूसरे तक फैली हुई हैं। घन 3D है, इसलिए इसके प्रत्येक कोने में 3 रेखाएँ हैं जो इससे उतरती हैं। इसी तरह, टेस्सेक्ट एक 4D आकार है, इसलिए प्रत्येक कोने से 4 रेखाएँ फैली हुई हैं।

टेस्सेक्ट की कल्पना करना कठिन क्यों है?

चूंकि हम, मनुष्य के रूप में, तीन आयामों में वस्तुओं की कल्पना करने के लिए विकसित हुए हैं, जो कुछ भी अतिरिक्त आयामों जैसे 4D, 5D, 6D, आदि में जाता है, हमारे लिए बहुत मायने नहीं रखता है, क्योंकि हमारे पास वे बिल्कुल भी नहीं हो सकते हैं। कल्पना करना। हमारा दिमाग अंतरिक्ष में चौथे आयाम को नहीं समझ सकता है। हम इसके बारे में सोच ही नहीं सकते।

अंक (± 1, ± 1, ± 1, ± 1)। दूसरे शब्दों में, इसे निम्नलिखित सेट के रूप में दर्शाया जा सकता है:

टेस्सेक्ट आठ हाइपरप्लेन से घिरा है, जिसका प्रतिच्छेदन टेस्सेक्ट के साथ ही इसके त्रि-आयामी चेहरों (जो साधारण क्यूब्स हैं) को परिभाषित करता है। गैर-समानांतर 3D चेहरों की प्रत्येक जोड़ी 2D फलक (वर्ग) बनाने के लिए प्रतिच्छेद करती है, और इसी तरह। अंत में, टेस्सेक्ट में 8 3D चेहरे, 24 2D, 32 किनारे और 16 कोने हैं।

प्रक्षेपण

द्वि-आयामी अंतरिक्ष में

यह संरचना कल्पना के लिए कठिन है, लेकिन एक टेसरेक्ट को दो-आयामी या त्रि-आयामी रिक्त स्थान में प्रोजेक्ट करना संभव है। इसके अलावा, विमान के प्रक्षेपण से हाइपरक्यूब के शीर्षों के स्थान को समझना आसान हो जाता है। इस तरह, छवियां प्राप्त की जा सकती हैं जो अब टेसरैक्ट के भीतर स्थानिक संबंधों को प्रतिबिंबित नहीं करती हैं, लेकिन जो निम्न उदाहरणों में शीर्ष कनेक्शन की संरचना को दर्शाती हैं:

तीसरी तस्वीर निर्माण बिंदु के सापेक्ष, आइसोमेट्रिक दृश्य में टेसरैक्ट दिखाती है। समानांतर कंप्यूटिंग में कई प्रोसेसर को जोड़ने के लिए एक टोपोलॉजिकल नेटवर्क के आधार के रूप में टेसरेक्ट का उपयोग करते समय यह दृश्य रुचि का है।

त्रि-आयामी अंतरिक्ष में

त्रि-आयामी अंतरिक्ष पर टेसरैक्ट के अनुमानों में से एक को दो नेस्टेड त्रि-आयामी क्यूब्स द्वारा दर्शाया गया है, जिनमें से संबंधित शिखर खंडों से जुड़े हुए हैं। त्रि-आयामी अंतरिक्ष में आंतरिक और बाहरी क्यूब्स के अलग-अलग आकार होते हैं, लेकिन चार-आयामी अंतरिक्ष में वे बराबर क्यूब्स होते हैं। टेस्सेक्ट के सभी क्यूब्स की समानता को समझने के लिए, एक घूर्णन टेस्सेक्ट मॉडल बनाया गया था।

टेसेरैक्ट के किनारों पर छह काटे गए पिरामिड समान छह क्यूब्स के चित्र हैं। हालांकि, ये क्यूब टेसरेक्ट के लिए हैं - जैसे वर्ग (चेहरे) से क्यूब तक। लेकिन वास्तव में, टेस्सेक्ट को अनंत संख्या में क्यूब्स में विभाजित किया जा सकता है, जैसे क्यूब - अनंत संख्या में वर्गों में, या एक वर्ग - अनंत संख्या में खंडों में।

त्रि-आयामी अंतरिक्ष पर टेसेरैक्ट का एक और दिलचस्प प्रक्षेपण एक समचतुर्भुज डोडेकेहेड्रॉन है, जिसके चार विकर्ण खींचे गए हैं, जो बड़े समचतुर्भुज कोणों पर विपरीत कोने के जोड़े को जोड़ते हैं। इस मामले में, टेसेरैक्ट के 16 में से 14 कोने रंबोडोडेकेड्रोन के 14 कोने में प्रक्षेपित होते हैं, और शेष 2 के अनुमान इसके केंद्र में मेल खाते हैं। त्रि-आयामी अंतरिक्ष पर इस तरह के प्रक्षेपण में, सभी एक-आयामी, दो-आयामी और त्रि-आयामी पक्षों की समानता और समानता संरक्षित होती है।

स्टीरियो जोड़ी

एक टेसेरैक्ट के स्टीरियोपेयर को त्रि-आयामी अंतरिक्ष पर दो अनुमानों के रूप में दर्शाया गया है। इस टेस्सेक्ट छवि को चौथे आयाम के रूप में गहराई का प्रतिनिधित्व करने के लिए डिज़ाइन किया गया था। एक स्टीरियोपेयर देखा जाता है ताकि प्रत्येक आंख इन छवियों में से केवल एक को देख सके, एक त्रिविम चित्र प्रकट होता है जो टेस्सेक्ट की गहराई को पुन: उत्पन्न करता है।

टेस्सेक्ट को खोलना

एक टेसरैक्ट की सतह को आठ क्यूब्स में विस्तारित किया जा सकता है (इसी तरह एक क्यूब की सतह को छह वर्गों में कैसे बढ़ाया जा सकता है)। 261 विभिन्न टेस्सेक्ट सामने आ रहे हैं। टेस्सेक्ट के प्रकट होने की गणना ग्राफ पर जुड़े हुए कोनों को खींचकर की जा सकती है।

कला में टेस्सेक्ट

एडविन ए के न्यू एबॉट प्लेन्स में, हाइपरक्यूब कहानीकार है।
द एडवेंचर्स ऑफ जिमी न्यूट्रॉन के एक एपिसोड में, "जीनियस बॉय" जिमी ने रॉबर्ट हेनलेन के उपन्यास "रोड टू ग्लोरी" (1963) के फोल्डबॉक्स के समान एक चार-आयामी हाइपरक्यूब का आविष्कार किया।
रॉबर्ट ई. हेनलेन ने कम से कम तीन विज्ञान कथा कहानियों में हाइपरक्यूब का उल्लेख किया है। "द हाउस ऑफ फोर डायमेंशन्स" ("द हाउस दैट टील बिल्ट") में, उन्होंने एक घर को एक टेसेरैक्ट के विकास के रूप में वर्णित किया, और फिर, भूकंप के कारण, चौथे आयाम में "गया" और "वास्तविक" बन गया "टेसेरैक्ट।
हेनलेन के उपन्यास रोड ऑफ ग्लोरी में एक बड़े आकार के बॉक्स का वर्णन किया गया है जो बाहर की तुलना में अंदर से बड़ा था।
हेनरी कुट्टनर की कहानी "ऑल टेनल्स ऑफ द बोरोगोव्स" दूर के भविष्य के बच्चों के लिए एक शैक्षिक खिलौने का वर्णन करती है, जो संरचना में एक टेसेरैक्ट के समान है।
एलेक्स गारलैंड () के उपन्यास में, "टेसरैक्ट" शब्द का प्रयोग चार-आयामी हाइपरक्यूब के त्रि-आयामी खुलासा के लिए किया जाता है, न कि हाइपरक्यूब। यह एक रूपक है जिसे यह दिखाने के लिए डिज़ाइन किया गया है कि संज्ञानात्मक प्रणाली को संज्ञेय की तुलना में व्यापक होना चाहिए।
घन 2: हाइपरक्यूब एक हाइपरक्यूब, या परस्पर जुड़े घनों के नेटवर्क में फंसे आठ अजनबियों पर ध्यान केंद्रित करता है।
टीवी श्रृंखला एंड्रोमेडा एक साजिश उपकरण के रूप में टेसेरैक्ट जनरेटर का उपयोग करती है। वे मुख्य रूप से स्थान और समय में हेरफेर करने के लिए डिज़ाइन किए गए हैं।
सल्वाडोर डाली () द्वारा पेंटिंग "क्रूसीफिक्सियन" (कॉर्पस हाइपरक्यूबस)।
नेक्स्टवेव कॉमिक बुक में एक वाहन को दर्शाया गया है जिसमें 5 टेसेरैक्ट जोन शामिल हैं।
वोइवोड नथिंगफेस एल्बम पर, गीतों में से एक को "इन माय हाइपरक्यूब" कहा जाता है।
एंथोनी पियर्स "रूट क्यूबा" के उपन्यास में अंतर्राष्ट्रीय विकास संघ के परिक्रमा करने वाले चंद्रमाओं में से एक को एक टेसेरैक्ट कहा जाता है, जिसे 3 आयामों में संकुचित किया गया था।
तीसरे सीज़न में "स्कूल" ब्लैक होल "श्रृंखला में" टेसेरैक्ट "श्रृंखला है। लुकास एक गुप्त बटन दबाता है और स्कूल "गणितीय टेसेरैक्ट की तरह आकार लेना" शुरू कर देता है।
शब्द "टेसेरैक्ट" और इससे प्राप्त शब्द "टेसेरैक्ट" मेडेलीन ल'एंगल की कहानी "द फोल्ड ऑफ टाइम" में पाए जाते हैं।
TesseracT एक ब्रिटिश सज्जन समूह का नाम है।
मार्वल सिनेमैटिक यूनिवर्स फिल्म श्रृंखला में, टेसरैक्ट एक प्रमुख कथानक तत्व है, जो एक हाइपरक्यूब के आकार का एक ब्रह्मांडीय विरूपण साक्ष्य है।
रॉबर्ट शेकली की कहानी "मिस माउस एंड द फोर्थ डायमेंशन" में, एक गूढ़ लेखक, लेखक का एक परिचित, एक टेसेरैक्ट को देखने की कोशिश करता है, जो उसके द्वारा बनाए गए उपकरण पर घंटों तक देखता है: एक स्टेम पर एक गेंद जिसमें छड़ें चिपकी होती हैं, जिस पर क्यूब्स लगाए जाते हैं, सभी गूढ़ प्रतीकों के साथ चिपकाए जाते हैं। कहानी में हिंटन के काम का उल्लेख है।
फिल्मों में कैप्टन अमेरिका: द एवेंजर्स। पूरे ब्रह्मांड की टेसरैक्ट-ऊर्जा

अन्य नामों

हेक्साडेकाहोरोन (इंग्लैंड। हेक्साडेकैचोरोन)
ऑक्टोहोरोन (इंग्लैंड। ऑक्टाकोरोन)
टेट्राक्यूबस
4-क्यूब
हाइपरक्यूब (यदि माप की संख्या निर्दिष्ट नहीं है)

नोट्स (संपादित करें)

साहित्य

चार्ल्स एच. हिंटन। चौथा आयाम, 1904। आईएसबीएन 0-405-07953-2
मार्टिन गार्डनर, मैथमैटिकल कार्निवल, 1977. ISBN 0-394-72349-X
इयान स्टीवर्ट, आधुनिक गणित की अवधारणाएं, 1995। आईएसबीएन 0-486-28424-7

लिंक

रूसी में

ट्रांसफॉर्मेटर4डी प्रोग्राम। चार-आयामी वस्तुओं (हाइपरक्यूब सहित) के त्रि-आयामी अनुमानों के मॉडल का निर्माण।
एक प्रोग्राम जो सी ++ में स्रोतों के साथ एक टेसेरैक्ट और उसके सभी एफ़िन परिवर्तनों के निर्माण को लागू करता है।

अंग्रेजी में

मशवेयर लिमिटेड - टेसेरैक्ट इंट्रेंस प्रोग्राम ( टेसेरैक्ट ट्रेनर, GPLv2 के साथ संगत लाइसेंस) और चार-आयामी अंतरिक्ष में प्रथम-व्यक्ति शूटर ( अदानैक्सिस; ग्राफिक्स, ज्यादातर त्रि-आयामी; ओएस रिपॉजिटरी में जीपीएल के तहत एक संस्करण है)।

बहुकोणीय आकृति

सही
(प्लेटोनिक ठोस)

तारकीय डोडेकाहेड्रॉन तारकीय इकोसिडोडेकाहेड्रॉन तारकीय इकोसाहेड्रोन तारकीय पॉलीहेड्रॉन तारकीय ऑक्टाहेड्रोन

उत्तल

आर्किमिडीयन निकाय	क्यूबोक्टाहेड्रोन इकोसिडोडेकेहेड्रॉन काटे गए टेट्राहेड्रोन काटे गए ऑक्टाहेड्रोन एंटी-ट्रंकेटेड इकोसाहेड्रोन काटे गए क्यूब काटे गए डोडेकाहेड्रोन रोम्बोक्यूबोक्टेहेड्रॉन रोम्बोइकोसोडोडेकेड्रोन रॉम्बो-ट्रंकेटेड क्यूबोक्टाहेड्रोन रोम्बो-ट्रंकेटेड क्यूबोकेटेड क्यूबोक्टेड क्यूबोक्टेड क्यूबोकेटेड डोडेकेटेड क्यूबोक्टेड
कैटलन निकाय	रंबोडोडेकाहेड्रोन रंबोट्रियाकोंटाहेड्रोन त्रिआकिस्टेराहेड्रोन टेट्राकिशेक्साहेड्रोन पेंटाकिसडोडेकाहेड्रॉन त्रिआकिसोक्टाहेड्रोन ट्राइकिसाइकोसाहेड्रोन
कोई पूर्ण स्थानिक समरूपता नहीं	पिरामिड प्रिज्म बिपिरामिड एंटीप्रिज्म ज़ोनोहेड्रोन पैरेललेपिपेड रॉम्बोहेड्रोन प्रिज्माटॉइड ट्रंकेटेड पिरामिड
पेंटागोंडोडेकेहेड्रॉन समांतरोहेड्रोन

सूत्र,
प्रमेय,
सिद्धांत

अन्य

हाइपरक्यूब और प्लेटोनिक सॉलिड्स

"वेक्टर" सिस्टम में एक काटे गए icosahedron ("सॉकर बॉल") का अनुकरण करें
जिसमें प्रत्येक पंचभुज षट्भुज से घिरा होता है

कटा हुआ इकोसाहेड्रोननियमित पंचभुज के रूप में फलकों के निर्माण के साथ 12 शीर्षों को काटकर प्राप्त किया जा सकता है। इस स्थिति में, नए पॉलीहेड्रॉन के शीर्षों की संख्या 5 गुना (12 × 5 = 60) बढ़ जाती है, 20 त्रिकोणीय फलक नियमित षट्भुज में बदल जाते हैं (कुल मिलाकर) फलक 20 + 12 = 32 . हो जाते हैं), ए किनारों की संख्या बढ़कर 30 + 12 × 5 = 90 . हो जाती है.

वेक्टर सिस्टम में एक काटे गए icosahedron के निर्माण के लिए कदम

4-आयामी अंतरिक्ष में आकार।

--à

--à ?

उदाहरण के लिए, एक घन और एक हाइपरक्यूब दिया गया है। एक हाइपरक्यूब में 24 फलक होते हैं। इसका मतलब है कि एक 4-आयामी ऑक्टाहेड्रोन में 24 कोने होंगे। हालांकि नहीं, एक हाइपरक्यूब में घनों के 8 फलक होते हैं - प्रत्येक केंद्र में एक शीर्ष होता है। इसका मतलब है कि एक 4-आयामी ऑक्टाहेड्रोन में 8 कोने होंगे जो आसान होते हैं।

4-आयामी अष्टफलक... इसमें आठ समबाहु और समान चतुष्फलक होते हैं,
प्रत्येक शीर्ष पर चार से जुड़ा हुआ है।

चावल। अनुकरण करने का प्रयास
"वेक्टर" प्रणाली में हाइपरस्फीयर-हाइपरस्फीयर

सामने - पीछे के चेहरे - बिना विरूपण के गेंदें। छह और गेंदें - आप दीर्घवृत्त या द्विघात सतहों (जनरेटर के रूप में 4 समोच्च रेखाओं के माध्यम से) या चेहरों के माध्यम से (पहले जनरेटर के माध्यम से निर्दिष्ट) निर्दिष्ट कर सकते हैं।

हाइपरस्फीयर को "बिल्ड" करने के लिए और ट्रिक्स
- 4-आयामी अंतरिक्ष में वही "सॉकर बॉल"

परिशिष्ट 2

उत्तल पॉलीहेड्रा के लिए, एक संपत्ति है जो इसके कोने, किनारों और चेहरों की संख्या को जोड़ती है, जिसे 1752 में लियोनार्ड यूलर द्वारा सिद्ध किया गया था, और इसे यूलर का प्रमेय कहा जाता है।

इसे तैयार करने से पहले, उन पॉलीटॉप्स पर विचार करें जिन्हें हम जानते हैं और निम्न तालिका में भरें, जिसमें बी शिखरों की संख्या है, पी किनारों है, और जी किसी दिए गए पॉलीटॉप के चेहरे हैं:

पॉलीहेड्रॉन नाम
त्रिकोणीय पिरामिड
चतुर्भुज पिरामिड
त्रिकोणीय प्रिज्म
चतुर्भुज प्रिज्म
एन -कोयला पिरामिड	एन+1	2एन	एन+1
एन -कार्बन प्रिज्म	2एन	3एन	एन + 2
एन -कोयला काट दिया पिरामिड	2एन	3एन	एन + 2

इस तालिका से यह प्रत्यक्ष रूप से देखा जाता है कि सभी चयनित पॉलीटोप्स के लिए समानता बी - पी + = 2 रखती है। यह पता चला है कि यह समानता न केवल इन पॉलीहेड्रा के लिए मान्य है, बल्कि एक मनमाना उत्तल पॉलीहेड्रॉन के लिए भी मान्य है।

यूलर का प्रमेय। किसी भी उत्तल पॉलीटोप के लिए, समानता

बी - आर + जी = 2,

जहाँ B शीर्षों की संख्या है, P किनारों की संख्या है, और G किसी दिए गए बहुफलक के फलकों की संख्या है।

सबूत।इस समानता को साबित करने के लिए, हम एक लोचदार सामग्री से बने दिए गए पॉलीहेड्रॉन की सतह का प्रतिनिधित्व करते हैं। आइए इसके एक फलक को हटा दें (काट लें) और शेष सतह को समतल पर फैला दें। हमें एक बहुभुज (बहुफलक के दूर फलक के किनारों द्वारा निर्मित) प्राप्त होता है, जिसे छोटे बहुभुजों में विभाजित किया जाता है (बहुफलक के अन्य फलकों द्वारा निर्मित)।

ध्यान दें कि बहुभुज विकृत, बढ़े हुए, कम किए जा सकते हैं, या यहां तक कि उनके पक्षों पर घुमावदार भी हो सकते हैं, जब तक कि भुजाएं नहीं टूटतीं। यह कोने, किनारों और चेहरों की संख्या नहीं बदलता है।

आइए हम साबित करें कि एक बहुभुज के छोटे बहुभुजों में परिणामी विभाजन के लिए, समानता

(*) बी - आर + जी "= 1,

जहां शीर्षों की कुल संख्या है, किनारों की कुल संख्या है, और Г "विभाजन में शामिल बहुभुजों की संख्या है। यह स्पष्ट है कि Г" = Г-1, जहां एक के फलकों की संख्या है पॉलीहेड्रॉन दिया।

आइए हम साबित करें कि दिए गए विभाजन के किसी बहुभुज में एक विकर्ण खींचे जाने पर समानता (*) नहीं बदलती है (चित्र 5, ए)। दरअसल, नए विभाजन में इस तरह के एक विकर्ण को खींचने के बाद बी शिखर, पी + 1 किनारों होंगे, और बहुभुजों की संख्या एक से बढ़ जाएगी। इसलिए, हमारे पास है

बी - (पी + 1) + (जी "+1) = बी - पी + जी" .

इस गुण का उपयोग करके, हम आने वाले बहुभुजों को त्रिभुजों में विभाजित करने वाले विकर्ण खींचते हैं, और परिणामी विभाजन के लिए हम दिखाते हैं कि समानता (*) संतुष्ट है (चित्र 5, बी)। ऐसा करने के लिए, हम त्रिभुजों की संख्या को कम करते हुए, बाहरी किनारों को लगातार हटाते रहेंगे। इस मामले में, दो मामले संभव हैं:

ए) त्रिकोण को हटाने के लिए एबीसीहमारे मामले में, दो पसलियों को निकालना आवश्यक है अबतथा ईसा पूर्व;

बी) त्रिकोण को हटाने के लिएएमकेएनहमारे मामले में, एक किनारे को हटाना आवश्यक हैएम.एन..

दोनों ही मामलों में, समानता (*) नहीं बदलेगी। उदाहरण के लिए, पहले मामले में, त्रिभुज को हटाने के बाद, ग्राफ़ में B - 1 कोने, P - 2 किनारे और G "- 1 बहुभुज शामिल होंगे:

(बी -1) - (पी + 2) + (जी "- 1) = बी - पी + जी"।

दूसरे मामले पर आप स्वयं विचार करें।

इस प्रकार, एक त्रिभुज को हटाने से समता (*) में कोई परिवर्तन नहीं होता है। त्रिभुजों को हटाने की इस प्रक्रिया को जारी रखते हुए, हम एक त्रिभुज के विभाजन के साथ समाप्त होते हैं। इस तरह के विभाजन के लिए, बी = 3, पी = 3, "= 1 और, इसलिए, बी - पी + Γ" = 1। इसलिए, समानता (*) मूल विभाजन के लिए भी है, जहां से हम अंत में एक के लिए प्राप्त करते हैं बहुभुज समानता (*) का दिया गया विभाजन सत्य है। इस प्रकार, मूल उत्तल पॉलीटोप के लिए, समानता B - P + = 2 सत्य है।

एक बहुफलक का उदाहरण जिसके लिए यूलर का संबंध नहीं है,चित्र 6 में दिखाया गया है। इस बहुफलक में 16 शीर्ष, 32 किनारे और 16 फलक हैं। इस प्रकार, इस बहुफलक के लिए, समानता B - P + = 0 रखती है।

परिशिष्ट 3.

फिल्म क्यूब 2: हाइपरक्यूब "(इंग्लैंड। क्यूब 2: हाइपरक्यूब) - एक शानदार फिल्म, फिल्म" क्यूब "की निरंतरता।

घन के आकार के कमरों में आठ अजनबी जागते हैं। कमरे चार-आयामी हाइपरक्यूब के अंदर स्थित हैं। कमरे लगातार "क्वांटम टेलीपोर्टेशन" द्वारा आगे बढ़ रहे हैं, और यदि आप अगले कमरे में चढ़ते हैं, तो पुराने में लौटने की संभावना नहीं है। एक हाइपरक्यूब में, समानांतर दुनिया एक दूसरे को काटती है, कुछ कमरों में अलग-अलग तरीकों से समय बहता है, और कुछ कमरे मौत के जाल हैं।

चित्र का कथानक मोटे तौर पर पहले भाग के इतिहास को दोहराता है, जो कुछ पात्रों की छवियों में भी परिलक्षित होता है। हाइपरक्यूब के विनाश के सटीक समय की गणना करने वाले नोबेल पुरस्कार विजेता रोसेनज़वेग का हाइपरक्यूब के कमरों में निधन हो गया.

आलोचना

अगर पहले भाग में भूलभुलैया में कैद लोगों ने एक-दूसरे की मदद करने की कोशिश की, तो इस फिल्म में हर आदमी अपने लिए है। बहुत सारे अनावश्यक विशेष प्रभाव हैं (वे जाल हैं) जो तार्किक रूप से फिल्म के इस हिस्से को पिछले वाले से नहीं जोड़ते हैं। यानी फिल्म क्यूब 2 निकली - यह भविष्य की 2020-2030 की एक तरह की भूलभुलैया है, लेकिन 2000 की नहीं। पहले भाग में, सैद्धांतिक रूप से एक व्यक्ति द्वारा सभी प्रकार के जाल बनाए जा सकते हैं। दूसरे भाग में, ये जाल एक कंप्यूटर प्रोग्राम हैं, तथाकथित "वर्चुअल रियलिटी"।

तस्वीरों के साथ घर का बना बेकिंग रेसिपी - स्टेप बाय स्टेप मास्टर क्लास