In geometry hypercube- this is n-dimensional analogy of the square ( n= 2) and cube ( n= 3). It is a closed, convex shape made up of groups of parallel lines located at opposite edges of the shape, and connected to each other at right angles.

This figure is also known as tesseract(tesseract). Tesseract refers to a cube as a cube refers to a square. More formally, a tesseract can be described as a regular convex four-dimensional polytope (polytope) whose boundary consists of eight cubic cells.

According to the Oxford English Dictionary, tesseract was coined in 1888 by Charles Howard Hinton and used in his book A New Era of Thought. The word was formed from the Greek "τεσσερες ακτινες" ("four rays"), there are four axes of coordinates. In addition, in some sources, the same figure was called tetracube(tetracube).

n-dimensional hypercube is also called n-cube.

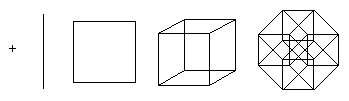
A point is a hypercube of dimension 0. If you move a point by a unit of length, you get a segment of unit length - a hypercube of dimension 1. Further, if you move a segment by a unit of length in the direction perpendicular to the direction of the segment, you get a cube - a hypercube of dimension 2. Shifting a square by a unit of length in the direction perpendicular to the plane of the square, a cube is obtained - a hypercube of dimension 3. This process can be generalized to any number of dimensions. For example, if you move a cube one unit of length in the fourth dimension, you get a tesseract.

The family of hypercubes is one of the few regular polyhedra that can be represented in any dimension.

Hypercube elements

Dimension hypercube n has 2 n"sides" (one-dimensional line has 2 points; two-dimensional square - 4 sides; three-dimensional cube - 6 faces; four-dimensional tesseract - 8 cells). The number of vertices (points) of the hypercube is 2 n(for example, for a cube - 2 3 vertices).

Quantity m-dimensional hypercubes on the border n-cube equals

For example, the border of a hypercube contains 8 cubes, 24 squares, 32 edges, and 16 vertices.

Elements of hypercubes

n-cube	Name	Vertex (0-edge)	Edge (1-side)	Edge (2-side)	Cell (3-side)	(4-side)	(5-side)	(6-side)	(7-side)	(8-side)
0-cube	Point	1
1-cube	Section	2	1
2-cube	Square	4	4	1
3-cube	Cube	8	12	6	1
4-cube	Tesseract	16	32	24	8	1
5-cube	Penterakt	32	80	80	40	10	1
6-cube	Hexeract	64	192	240	160	60	12	1
7-cube	Hepteract	128	448	672	560	280	84	14	1
8-cube	Octract	256	1024	1792	1792	1120	448	112	16	1
9-cube	Generact	512	2304	4608	5376	4032	2016	672	144	18

Plane projection

The formation of a hypercube can be represented in the following way:

• Two points A and B can be connected to form a line segment AB.
• Two parallel line segments AB and CD can be connected to form a square ABCD.
• Two parallel squares ABCD and EFGH can be connected to form a cube ABCDEFGH.
• Two parallel cubes ABCDEFGH and IJKLMNOP can be connected to form the hypercube ABCDEFGHIJKLMNOP.

The latter structure is not easy to imagine, but it is possible to depict its projection onto a 2D or 3D space. Moreover, projections onto a 2D plane can be more useful by being able to rearrange the positions of the projected vertices. In this case, you can get images that no longer reflect the spatial relationships of elements within the tesseract, but illustrate the structure of vertex connections, as in the examples below.

The first illustration shows how, in principle, a tesseract is formed by joining two cubes. This diagram is similar to the diagram for creating a two-square cube. The second diagram shows that all the edges of the tesseract have the same length. This scheme also forces you to search for cubes connected to each other. In the third diagram, the vertices of the tesseract are located in accordance with the distances along the edges relative to the bottom point. This scheme is interesting in that it is used as a basic scheme for the network topology of connecting processors when organizing parallel computing: the distance between any two nodes does not exceed 4 edge lengths, and there are many different ways to balance the load.

Hypercube in art

The hypercube has appeared in science fiction literature since 1940, when Robert Heinlein, in his story "And He Built a Crooked House", described a house built in the shape of a tesseract sweep. In the story, this Further, this house collapses, turning into a four-dimensional tesseract. After that, the hypercube appears in many books and novels.

The movie "Cube 2: Hypercube" tells the story of eight people trapped in a network of hypercubes.

The painting by Salvador Dali "The Crucifixion" ("Crucifixion (Corpus Hypercubus)", 1954) depicts Jesus crucified on a tesseract scan. This painting can be seen at the Metropolitan Museum of Art in New York.

Conclusion

The hypercube is one of the simplest four-dimensional objects, by the example of which you can see all the complexity and unusualness of the fourth dimension. And what looks impossible in three dimensions, possibly in four, for example, impossible figures. So, for example, the bars of an impossible triangle in four dimensions will be connected at right angles. And this figure will look like this from all points of view, and will not be distorted, unlike the realizations of the impossible triangle in three-dimensional space (see.

If an unusual incident happened to you, you saw a strange creature or an incomprehensible phenomenon, you had an unusual dream, you saw a UFO in the sky or became a victim of an alien abduction, you can send us your story and it will be published on our website ===> .

The doctrine of multidimensional spaces began to appear in the middle of the 19th century. Scientists borrowed the idea of ​​four-dimensional space from scientists. In their works, they told the world about the amazing wonders of the fourth dimension.

The heroes of their works, using the properties of four-dimensional space, could eat the contents of an egg without damaging the shell, drink a drink without opening the bottle cap. The thieves recovered the treasure from the safe through the fourth dimension. Surgeons performed operations on internal organs without cutting the patient's body tissue.

Tesseract

In geometry, a hypercube is an n-dimensional analogy of a square (n = 2) and a cube (n = 3). The four-dimensional analogue of our usual three-dimensional cube is known as tesseract. Tesseract refers to a cube as a cube refers to a square. More formally, a tesseract can be described as a regular convex four-dimensional polyhedron whose boundary consists of eight cubic cells.

Each pair of non-parallel 3D faces intersect to form 2D faces (squares), and so on. Finally, a tesseract has 8 3D faces, 24 2D, 32 edges, and 16 vertices.
By the way, according to the Oxford Dictionary, the word tesseract was coined and used in 1888 by Charles Howard Hinton (1853-1907) in his book A New Age of Thought. Later, some people called the same figure a tetracubus (Greek tetra - four) - a four-dimensional cube.

Construction and description

Let's try to imagine what the hypercube will look like without leaving three-dimensional space.
In one-dimensional "space" - on a line - select a segment AB of length L. On a two-dimensional plane at a distance L from AB, draw a segment DC parallel to it and connect their ends. The result is a square CDBA. Repeating this operation with the plane, we get a three-dimensional cube CDBAGHFE. And shifting the cube in the fourth dimension (perpendicular to the first three) by a distance L, we get the hypercube CDBAGHFEKLJIOPNM.

In a similar way, we can continue the reasoning for hypercubes of a larger number of dimensions, but it is much more interesting to see how a four-dimensional hypercube will look like for us, inhabitants of three-dimensional space.

Take a wire cube ABCDHEFG and look at it with one eye from the side of the face. We will see and can draw two squares on the plane (its near and far faces), connected by four lines - side edges. Similarly, a four-dimensional hypercube in three-dimensional space will look like two cubic "boxes" inserted into each other and connected by eight edges. In this case, the "boxes" themselves - three-dimensional faces - will be projected onto "our" space, and the lines connecting them will stretch in the direction of the fourth axis. You can also try to imagine a cube not in projection, but in a spatial image.

Just as a three-dimensional cube is formed by a square shifted by the length of a face, a cube shifted into the fourth dimension will form a hypercube. It is limited by eight cubes, which in perspective will look like a rather complex figure. The very same four-dimensional hypercube can be broken into an infinite number of cubes, just as a three-dimensional cube can be "cut" into an infinite number of flat squares.

Having cut six faces of a three-dimensional cube, you can expand it into a flat shape - a sweep. It will have a square on each side of the original face plus one more - the face opposite to it. And the three-dimensional unfolding of the four-dimensional hypercube will consist of the original cube, six cubes "growing" from it, plus one more - the final "hyperface".

Hypercube in art

The Tesseract is such an interesting figure that it has repeatedly attracted the attention of writers and filmmakers.
Robert E. Heinlein mentioned hypercubes several times. In The House That Teale Built (1940), he described a house built as a development of a tesseract, and then, due to an earthquake, "formed" in the fourth dimension and became a "real" tesseract. Heinlein's novel Road of Glory describes an oversized box that was larger on the inside than on the outside.

Henry Kuttner's story "All tenals of the Borogovs" describes an educational toy for children from the distant future, similar in structure to a tesseract.

Cube 2: Hypercube focuses on eight strangers trapped in a hypercube, or network of interconnected cubes.

Parallel world

Mathematical abstractions gave rise to the idea of ​​the existence of parallel worlds. These are understood as realities that exist simultaneously with ours, but independently of it. A parallel world can be of various sizes, from a small geographic area to an entire universe. In a parallel world, events take place in their own way, it can differ from our world, both in individual details and in almost everything. Moreover, the physical laws of a parallel world are not necessarily analogous to the laws of our Universe.

This topic is fertile ground for science fiction writers.

The painting by Salvador Dali "Crucifixion" depicts a tesseract. "Crucifixion or Hypercubic Body" - a painting by the Spanish artist Salvador Dali, painted in 1954. Depicts the crucified Jesus Christ on a tesseract scan. The painting is kept at the Metropolitan Museum of Art in New York

It all began in 1895, when Herbert Wells revealed the existence of parallel worlds for fantasy with his story "A Door in a Wall". In 1923, Wells returned to the idea of ​​parallel worlds and placed in one of them a utopian country, where the characters of the novel People as Gods go.

The novel did not go unnoticed. In 1926, G. Dent's story "The Emperor of the Country" If "appeared in Dent's story. these are no less real than ours.

In 1944, Jorge Luis Borges published the story The Garden of Forking Paths in his book Fictional Stories. Here the idea of ​​time branching was finally expressed with the utmost clarity.
Despite the appearance of the above-listed works, the idea of ​​many-worlds began to seriously develop in science fiction only in the late forties of the XX century, at about the same time when a similar idea arose in physics.

One of the pioneers of a new direction in science fiction was John Bixby, who suggested in his story "One-Way Street" (1954) that between worlds you can only move in one direction - having gone from your world to a parallel one, you will not go back, but you will move from one world to the next. However, a return to one's own world is also not excluded - for this it is necessary that the system of worlds be closed.

Clifford Simak's novel "A Ring Around the Sun" (1982) describes numerous planets of the Earth, each existing in its own world, but in the same orbit, and these worlds and these planets differ from each other only by a slight (microsecond) shift in time ... The numerous lands visited by the hero of the novel form a single system of worlds.

Alfred Bester expressed an interesting look at the branching of worlds in the story "The Man Who Killed Mohammed" (1958). "Changing the past," the hero of the story argued, "you change it only for yourself." In other words, after a change in the past, a branch of history arises, in which this change exists only for the character who made the change.

The story of the Strugatsky brothers "Monday begins on Saturday" (1962) describes the travels of characters in different versions of the future described by science fiction writers - in contrast to the travels that already existed in science fiction to different versions of the past.

However, even a simple listing of all the works in which the topic of parallel worlds is touched upon would take too long. And although science fiction writers, as a rule, do not scientifically substantiate the postulate of multidimensionality, they are right about one thing - this is a hypothesis that has the right to exist.
The fourth dimension of the tesseract is still waiting for us.

Victor Savinov

If you are a fan of the Avengers movies, the first thing that comes to your mind when you hear the word "Tesseract" is the transparent cube-shaped vessel of the Infinity Stone containing boundless power.

For fans of the Marvel Universe, the Tesseract is a glowing blue cube that makes people from not only Earth, but other planets also go crazy. This is why all the Avengers have banded together to protect the Earthlings from the extremely destructive forces of the Tesseract.

However, the following must be said: The Tesseract is an actual geometric concept, or rather, a form that exists in 4D. This isn't just a blue cube from the Avengers ... it's a real concept.

The Tesseract is an object in 4 dimensions. But before we explain it in detail, let's start from the beginning.

What is dimension?

Everyone has heard the terms 2D and 3D, representing respectively two-dimensional or three-dimensional objects in space. But what are these?

Measurement is simply the direction you can go. For example, if you are drawing a line on a piece of paper, you can go either left / right (x-axis) or up / down (y-axis). Thus, we say that the paper is two-dimensional, since you can only walk in two directions.

There is a sense of depth in 3D.

Now, in the real world, besides the two directions mentioned above (left / right and up / down), you can also go to / from. Hence, a sense of depth is added in 3D space. Therefore, we say that real life is 3-dimensional.

A point can represent 0 dimensions (since it does not move in any direction), a line represents 1 dimension (length), a square represents 2 dimensions (length and width), and a cube represents 3 dimensions (length, width, and height).

Take a 3D cube and replace each face (which is currently a square) with a cube. And so! The shape you get is the tesseract.

What is a tesseract?

Simply put, a tesseract is a cube in 4-dimensional space. You can also say that it is a 4D analogue of a cube. It is a 4D shape where each face is a cube.

A 3D projection of a tesseract that rotates twice around two orthogonal planes.
Image: Jason Hise

Here's a simple way to conceptualize dimensions: a square is two-dimensional; therefore, each of its corners has 2 lines extending from it at an angle of 90 degrees to each other. The cube is 3D, so each of its corners has 3 lines descending from it. Likewise, the tesseract is a 4D shape, so each corner has 4 lines extending from it.

Why is it difficult to imagine a tesseract?

Since we, as humans, have evolved to visualize objects in three dimensions, anything that goes into extra dimensions such as 4D, 5D, 6D, etc., does not make much sense to us, because we cannot have them at all. imagine. Our brain cannot understand the 4th dimension in space. We just can't think about it.

Points (± 1, ± 1, ± 1, ± 1). In other words, it can be represented as the following set:

The tesseract is bounded by eight hyperplanes, the intersection of which with the tesseract itself defines its three-dimensional faces (which are ordinary cubes). Each pair of non-parallel 3D faces intersect to form 2D faces (squares), and so on. Finally, a tesseract has 8 3D faces, 24 2D, 32 edges, and 16 vertices.

Popular Description

Let's try to imagine what the hypercube will look like without leaving three-dimensional space.

In one-dimensional "space" - on a line - select a segment AB of length L. On a two-dimensional plane at a distance L from AB, draw a segment DC parallel to it and connect their ends. The result is a square CDBA. Repeating this operation with the plane, we get a three-dimensional cube CDBAGHFE. And shifting the cube in the fourth dimension (perpendicular to the first three) by a distance L, we get the hypercube CDBAGHFEKLJIOPNM.

Constructing a tesseract on a plane

The one-dimensional segment AB is the side of the two-dimensional square CDBA, the square is the side of the cube CDBAGHFE, which, in turn, will be the side of the four-dimensional hypercube. A straight line segment has two boundary points, a square has four vertices, and a cube has eight. Thus, in a four-dimensional hypercube, there will be 16 vertices: 8 vertices of the original cube and 8 shifted in the fourth dimension. It has 32 edges - 12 each give the initial and final positions of the original cube, and 8 more edges will "draw" its eight vertices, which have moved into the fourth dimension. The same reasoning can be done for the faces of the hypercube. In two-dimensional space, it is one (the square itself), the cube has 6 of them (two faces from the moved square and four more will describe its sides). A four-dimensional hypercube has 24 square faces - 12 squares of the original cube in two positions and 12 squares from its twelve edges.

As the sides of a square are 4 one-dimensional segments, and the sides (faces) of a cube are 6 two-dimensional squares, so for a "four-dimensional cube" (tesseract), the sides are 8 three-dimensional cubes. The spaces of opposite pairs of tesseract cubes (that is, the three-dimensional spaces to which these cubes belong) are parallel. In the figure, these are cubes: CDBAGHFE and KLJIOPNM, CDBAKLJI and GHFEOPNM, EFBAMNJI and GHDCOPLK, CKIAGOME and DLJBHPNF.

In a similar way, we can continue the reasoning for hypercubes of a larger number of dimensions, but it is much more interesting to see how a four-dimensional hypercube will look like for us, inhabitants of three-dimensional space. Let's use the familiar analogy method for this.

Take a wire cube ABCDHEFG and look at it with one eye from the side of the face. We will see and can draw two squares on the plane (its near and far faces), connected by four lines - side edges. Similarly, a four-dimensional hypercube in three-dimensional space will look like two cubic "boxes" inserted into each other and connected by eight edges. In this case, the "boxes" themselves - three-dimensional faces - will be projected onto "our" space, and the lines connecting them will stretch in the direction of the fourth axis. You can also try to imagine a cube not in projection, but in a spatial image.

Just as a three-dimensional cube is formed by a square shifted by the length of a face, a cube shifted into the fourth dimension will form a hypercube. It is limited by eight cubes, which in perspective will look like a rather complex figure. The very same four-dimensional hypercube consists of an infinite number of cubes, just as a three-dimensional cube can be "cut" into an infinite number of flat squares.

Having cut six faces of a three-dimensional cube, you can expand it into a flat shape - a sweep. It will have a square on each side of the original face plus one more - the face opposite to it. And the three-dimensional unfolding of the four-dimensional hypercube will consist of the original cube, six cubes "growing" from it, plus one more - the final "hyperface".

Tesseract properties are the continuation of the properties of geometric figures of lower dimensions into four-dimensional space.

Projection

Into two-dimensional space

This structure is difficult for the imagination, but it is possible to project a tesseract into 2D or 3D spaces. In addition, projection to plane makes it easy to understand the location of the vertices of the hypercube. In this way, images can be obtained that no longer reflect spatial relationships within the tesseract, but which illustrate the structure of vertex connections, as in the following examples:

The third picture shows the tesseract in isometric view, relative to the construction point. This view is of interest when using a tesseract as the basis for a topological network to link multiple processors in parallel computing.

Into three-dimensional space

One of the projections of the tesseract onto three-dimensional space is represented by two nested three-dimensional cubes, the corresponding vertices of which are connected by segments. The inner and outer cubes have different sizes in three-dimensional space, but in four-dimensional space they are equal cubes. To understand the equality of all the cubes of the tesseract, a rotating tesseract model was created.

• The six truncated pyramids at the edges of the tesseract are images of equal six cubes. However, these cubes are to a tesseract - like squares (faces) to a cube. But in fact, the tesseract can be divided into an infinite number of cubes, like a cube - into an infinite number of squares, or a square - into an infinite number of segments.

Another interesting projection of the tesseract onto three-dimensional space is a rhombic dodecahedron with its four diagonals drawn, connecting pairs of opposite vertices at large rhombus angles. In this case, 14 of the 16 vertices of the tesseract are projected into 14 vertices of the rhombododecahedron, and the projections of the remaining 2 coincide in its center. In such a projection onto a three-dimensional space, the equality and parallelism of all one-dimensional, two-dimensional and three-dimensional sides are preserved.

Stereo pair

A stereopair of a tesseract is depicted as two projections onto three-dimensional space. This tesseract image was designed to represent depth as a fourth dimension. A stereopair is viewed so that each eye sees only one of these images, a stereoscopic picture appears that reproduces the depth of the tesseract.

Unfolding the tesseract

The surface of a tesseract can be expanded into eight cubes (similar to how the surface of a cube can be expanded into six squares). There are 261 different tesseract unfolding. The unfolding of the tesseract can be calculated by drawing connected corners on the graph.

Tesseract in art

• In Edwine A.'s New Abbott Plains, the hypercube is the storyteller.
• In one episode of The Adventures of Jimmy Neutron, "genius boy" Jimmy invents a four-dimensional hypercube identical to the foldbox from the novel "Road to Glory" (1963) by Robert Heinlein.
• Robert E. Heinlein has mentioned hypercubes in at least three science fiction stories. In "The House of Four Dimensions" ("The House That Teal Built"), he described a house built as a development of a tesseract, and then, due to an earthquake, "formed" in the fourth dimension and became a "real" tesseract.
• Heinlein's novel Road of Glory describes an oversized box that was larger on the inside than on the outside.
• Henry Kuttner's story "All tenals of the Borogovs" describes an educational toy for children from the distant future, similar in structure to a tesseract.
• In the novel by Alex Garland (), the term "tesseract" is used for a three-dimensional unfolding of a four-dimensional hypercube, rather than the hypercube itself. This is a metaphor designed to show that the cognizing system should be broader than the cognizable one.
• Cube 2: Hypercube focuses on eight strangers trapped in a hypercube, or network of interconnected cubes.
• The TV series Andromeda uses tesseract generators as a conspiracy device. They are primarily designed to manipulate space and time.
• Painting "Crucifixion" (Corpus Hypercubus) by Salvador Dali ().
• The Nextwave comic book depicts a vehicle that includes 5 tesseract zones.
• On the Voivod Nothingface album, one of the songs is called “In my hypercube”.
• In the novel by Anthony Pierce "Route Cuba" one of the orbiting moons of the International Development Association is called a tesseract, which was compressed into 3 dimensions.
• In the series "School" Black Hole "" in the third season there is a series "Tesseract". Lucas pushes a secret button and the school begins to "take shape like a mathematical tesseract."
• The term "tesseract" and the term "tesserate", derived from it, is found in Madeleine L'Engle's story "The Fold of Time".
• TesseracT is the name of a British gentleman group.
• In the Marvel Cinematic Universe film series, the Tesseract is a key plot element, a space artifact shaped like a hypercube.
• In Robert Sheckley's story "Miss Mouse and the Fourth Dimension," one esoteric writer, an acquaintance of the author, tries to see a tesseract, looking for hours at a device he has constructed: a ball on a leg with rods stuck into it, on which cubes are planted, pasted over with all successive esoteric symbols. The story mentions Hinton's work.
• In the films Captain America: The Avengers. Tesseract-energy of the whole universe

Other names

• Hexadekahoron (eng. Hexadecachoron)
• Octohoron (eng. Octachoron)
• Tetracubus
• 4-Cube
• Hypercube (if the number of measurements is not specified)

Notes (edit)

Literature

• Charles H. Hinton. Fourth Dimension, 1904. ISBN 0-405-07953-2
• Martin Gardner, Mathmatical Carnival, 1977. ISBN 0-394-72349-X
• Ian Stewart, Concepts of Modern Mathematics, 1995. ISBN 0-486-28424-7

Links

In Russian

• Transformator4D program. Formation of models of three-dimensional projections of four-dimensional objects (including the Hypercube).
• A program that implements the construction of a tesseract and all its affine transformations, with sources in C ++.

In English

• Mushware Limited - Tesseract inference program ( Tesseract Trainer, license compatible with GPLv2) and first person shooter in four-dimensional space ( Adanaxis; graphics, mostly three-dimensional; there is a version under the GPL in the OS repositories).

Polyhedra
Correct (Platonic solids)
Stellated dodecahedron Stellated icosidodecahedron Stellated icosahedron Stellated polyhedron Stellated octahedron
Convex	Archimedean bodies Cuboctahedron Icosidodecahedron Truncated tetrahedron Truncated octahedron Anti-truncated icosahedron Truncated cube Truncated dodecahedron Rhombocuboctahedron Rhomboicosododecahedron Rhombo-truncated cuboctahedron Rhombo-truncated cuboctahedron Rhombo-truncated dodecahedron Truncated cuboidal cube Catalan Bodies Rhombododecahedron Rhombotriacontahedron Triakistetrahedron Tetrakishexahedron Pentakisdodecahedron Triakisoktahedron Triakisycosahedron Deltoidal icositetrahedron Deltoidal hexcontahedron Pentagonal icostetrahedron No full spatial symmetry Pyramid Prism Bipyramid Antiprism Zonohedron Parallelepiped Rhombohedron Prismatoid Truncated pyramid Pentagondodecahedron parallelohedron
Formulas, theorems, theory
Other

Hypercube and Platonic Solids

Simulate a truncated icosahedron ("soccer ball") in the "Vector" system
in which each pentagon is bounded by hexagons

Truncated icosahedron can be obtained by cutting off 12 vertices with the formation of faces in the form of regular pentagons. In this case, the number of vertices of the new polyhedron increases 5 times (12 × 5 = 60), 20 triangular faces turn into regular hexagons (in total faces become 20 + 12 = 32), a the number of edges increases to 30 + 12 × 5 = 90.

Steps for constructing a truncated icosahedron in the "Vector" system

Shapes in 4-dimensional space.

--à

--à ?

For example, given a cube and a hypercube. There are 24 faces in a hypercube. This means that a 4-dimensional octahedron will have 24 vertices. Although no, a hypercube has 8 faces of cubes - each has a center-vertex. This means that a 4-dimensional octahedron will have 8 vertices that are easier.

4-dimensional octahedron... It consists of eight equilateral and equal tetrahedrons,
connected by four at each vertex.

Rice. Attempt to simulate
hypersphere-hypersphere in the "Vector" system

Front - back faces - balls without distortion. Six more balls - you can specify through ellipsoids or quadratic surfaces (through 4 contour lines as generators) or through faces (first specified through generators).

More tricks to "build" a hypersphere
- the same "soccer ball" in 4-dimensional space

Appendix 2

For convex polytopes, there is a property that connects the number of its vertices, edges and faces, proved in 1752 by Leonard Euler, and called Euler's theorem.

Before formulating it, consider the polyhedra we know of and fill in the following table, in which B is the number of vertices, P is the edges, and G is the faces of a given polytope:

Polyhedron name
Triangular pyramid
Quadrangular pyramid
Triangular prism
Quadrangular prism
n -coal pyramid	n+1	2n	n+1
n -carbon prism	2n	3n	n + 2
n -coal truncated pyramid	2n	3n	n + 2

From this table it is directly seen that for all selected polytopes the equality B - P + Γ = 2 holds. It turns out that this equality is valid not only for these polyhedra, but also for an arbitrary convex polyhedron.

Euler's theorem. For any convex polytope, the equality

B - R + G = 2,

where B is the number of vertices, P is the number of edges, and G is the number of faces of a given polyhedron.

Proof. To prove this equality, we represent the surface of a given polyhedron made of an elastic material. Let's delete (cut out) one of its faces and stretch the remaining surface on a plane. We get a polygon (formed by the edges of the distant face of the polyhedron), divided into smaller polygons (formed by the other faces of the polyhedron).

Note that polygons can be deformed, enlarged, reduced, or even curved on their sides, as long as the sides do not break. This does not change the number of vertices, edges, and faces.

Let us prove that for the resulting partition of a polygon into smaller polygons, the following equality holds:

(*) B - R + G "= 1,

where В is the total number of vertices, Р is the total number of edges and Г "is the number of polygons included in the partition. It is clear that Г" = Г - 1, where Г is the number of faces of a given polyhedron.

Let us prove that equality (*) does not change if a diagonal is drawn in some polygon of the given partition (Fig. 5, a). Indeed, after drawing such a diagonal in the new partition there will be B vertices, P + 1 edges, and the number of polygons will increase by one. Therefore, we have

B - (P + 1) + (G "+1) = B - P + G" .

Using this property, we draw diagonals dividing the incoming polygons into triangles, and for the resulting partition we show that equality (*) is satisfied (Fig. 5, b). To do this, we will consistently remove the outer edges, reducing the number of triangles. In this case, two cases are possible:

a) to remove the triangle ABC it is required to remove two ribs, in our case AB and BC;

b) to remove the triangleMKNit is required to remove one edge, in our caseMN.

In both cases, the equality (*) will not change. For example, in the first case, after deleting the triangle, the graph will consist of B - 1 vertices, P - 2 edges and G "- 1 polygon:

(B - 1) - (R + 2) + (G "- 1) = B - R + G".

Consider the second case on your own.

Thus, removing one triangle does not change the equality (*). Continuing this process of deleting triangles, in the end, we come to a partition consisting of one triangle. For such a partition, B = 3, P = 3, Γ "= 1 and, therefore, B - P + Γ" = 1. Hence, equality (*) also holds for the original partition, whence we finally obtain that for a given partition of the polygon equality (*) is true. Thus, for the original convex polytope, the equality B - P + Γ = 2 is true.

An example of a polyhedron for which Euler's relation does not hold, shown in Figure 6. This polyhedron has 16 vertices, 32 edges, and 16 faces. Thus, for this polyhedron, the equality B - P + Γ = 0 holds.

Appendix 3.

Film Cube 2: Hypercube "(eng. Cube 2: Hypercube) - a fantastic film, the continuation of the film" Cube ".

Eight strangers wake up in cube-shaped rooms. The rooms are located inside a four-dimensional hypercube. Rooms are constantly moving by "quantum teleportation", and if you climb into the next room, then return to the old one is already unlikely. In a hypercube, parallel worlds intersect, time flows in some rooms in different ways, and some rooms are death traps.

The plot of the picture largely repeats the history of the first part, which is also reflected in the images of some of the characters. Nobel laureate Rosenzweig, who calculated the exact time of the destruction of the hypercube, dies in the rooms of the hypercube.

Criticism

If in the first part people imprisoned in a labyrinth tried to help each other, in this film it's every man for himself. There are a lot of unnecessary special effects (they are traps) that do not logically connect this part of the film with the previous one. That is, it turns out the film Cube 2 - this is a kind of maze of the future 2020-2030, but not 2000. In the first part, all kinds of traps can theoretically be created by a person. In the second part, these traps are a computer program, the so-called "Virtual Reality".